题目内容
如图已知点C为AB上一点,AC=12cm,CB=| 2 | 3 |

分析:求DE的长度,即求出AD和AE的长度.因为D、E分别为AC、AB的中点,故DE=
(AB-AC),又AC=12cm,CB=
AC,可求出CB,即可求出CB,代入上述代数式,即可求出DE的长度.
| 1 |
| 2 |
| 2 |
| 3 |
解答:解:根据题意,AC=12cm,CB=
AC,
所以CB=8cm,
所以AB=AC+CB=20cm,
又D、E分别为AC、AB的中点,
所以DE=AE-AD=
(AB-AC)=4cm.
即DE=4cm.
故答案为4cm.
| 2 |
| 3 |
所以CB=8cm,
所以AB=AC+CB=20cm,
又D、E分别为AC、AB的中点,
所以DE=AE-AD=
| 1 |
| 2 |
即DE=4cm.
故答案为4cm.
点评:此题要求学生灵活运用线段的和、差、倍、分之间的数量关系,熟练掌握.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
 AC,D、E分别为AC、AB的中点,求DE的长。
AC,D、E分别为AC、AB的中点,求DE的长。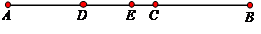

 AC,D、E分别为AC、AB的中点,求DE的长。
AC,D、E分别为AC、AB的中点,求DE的长。
 AC,D、E分别为AC、AB的中点,求DE的长。
AC,D、E分别为AC、AB的中点,求DE的长。
 AC,D、E分别为AC、AB的中点,求DE的长。
AC,D、E分别为AC、AB的中点,求DE的长。
