题目内容
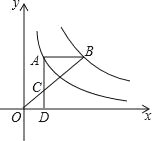
如图，点A在双曲线y=
上，点B在双曲线y=
（k≠0）上，AB∥x轴，过点A作AD⊥x轴 于D．连接OB，与AD相交于点C，若AC=2CD，则k的值为____．
练习册系列答案
期末集结号系列答案
相关题目
在学校开展的“争做最优秀中学生”的一次演讲比赛中，编号分别为1，2，3，4，5的五位同学最后成绩如下表所示：
参赛者编号 | 1 | 2 | 3 | 4 | 5 |
成绩（分） | 96 | 88 | 86 | 93 | 86 |
那么这五位同学演讲成绩的众数与中位数依次是（ ）
A. 96，88 B. 92，88 C. 88，86 D. 86，88
﹣
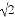）0+
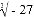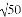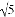+|2﹣
﹣
）÷
）（2﹣
，0），且与y轴相交于点C．
B. 
C. 
D. 
