题目内容
【题目】如图,△ABC中,∠BAC=110°,DE,FG分别为AB,AC的垂直平分线,E,G分别为垂足. 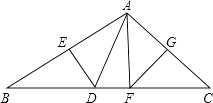
(1)求∠DAF的度数;
(2)如果BC=10cm,求△DAF的周长.
【答案】
(1)解:设∠B=x,∠C=y.
∵∠BAC+∠B+∠C=180°,
∴110°+∠B+∠C=180°,
∴x+y=70°.
∵AB、AC的垂直平分线分别交BA于E、交AC于G,
∴DA=BD,FA=FC,
∴∠EAD=∠B,∠FAC=∠C.
∴∠DAF=∠BAC﹣(x+y)=110°﹣70°=40°
(2)解:∵AB、AC的垂直平分线分别交BA于E、交AC于G,
∴DA=BD,FA=FC,
∴△DAF的周长为:AD+DF+AF=BD+DF+FC=BC=10(cm).
【解析】(1)根据三角形内角和定理可求∠B+∠C;根据垂直平分线性质,DA=BD,FA=FC,则∠EAD=∠B,∠FAC=∠C,得出∠DAF=∠BAC﹣∠EAD﹣∠FAC=110°﹣(∠B+∠C)求出即可.(2)由(1)中得出,AD=BD,AF=FC,即可得出△DAF的周长为BD+FC+DF=BC,即可得出答案.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目