题目内容
已知:△ABC的中线BD、CE交于点O,F、G分别是OB、OC的中点。
求证:四边形DEFG是平行四边形。
求证:四边形DEFG是平行四边形。

证明:∵中线BD,CE相交于O,
F,G分别为OB,OC的中点,
∴ED,FG 为中位线,
∵ED=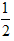 BC,
BC,
FG=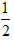 BC
BC
∴ED=FG
∵ED ∥BC
FG平行BC (三角形中位线平行于第三边)
∴ED∥FG
∵有一组对边平行且相等的四边形是平行四边形
∴四边形DEFG为平行四边形。
F,G分别为OB,OC的中点,
∴ED,FG 为中位线,
∵ED=
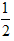 BC,
BC,FG=
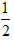 BC
BC ∴ED=FG
∵ED ∥BC
FG平行BC (三角形中位线平行于第三边)
∴ED∥FG
∵有一组对边平行且相等的四边形是平行四边形
∴四边形DEFG为平行四边形。

练习册系列答案
相关题目
 已知:△ABC的中线BD、CE交于点O,F、G分别是OB、OC的中点.
已知:△ABC的中线BD、CE交于点O,F、G分别是OB、OC的中点.