题目内容
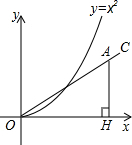如图，在第一象限内作射线OC，与x轴的夹角为30°，在射线OC上取一点A，过点A作AH⊥x轴于点H．在抛物线y=x2（x＞0）上取点P，在y轴上取点Q，使得以P，O，Q为顶点的三角形与△AOH全等，则符合条件的点A的坐标是分析：在△AOH中，因为∠AOH=30°，所以A的纵坐标是横坐标的
倍，若设A的坐标为（
t，t），则Q、P点坐标均可求出，然后根据全等三角形的判定，对应求解即可．
| 3 |
| 3 |
解答：解：由题可得A的横坐标是纵坐标的
倍，故设A的坐标为（
t，t）；
则Q的坐标为（0，2t）或（0，
t）；
可求得P点对应的坐标，解可得t的值有4个，为
，
，2，
；
故点A的坐标是（3，
）、（
，
）、（2
，2）、（
，
）．
| 3 |
| 3 |
则Q的坐标为（0，2t）或（0，
| 3 |
可求得P点对应的坐标，解可得t的值有4个，为
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
故点A的坐标是（3，
| 3 |
| 1 |
| 3 |
| 3 |
| 1 |
| 3 |
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
点评：本题考查二次函数的有关性质，涉及图象与点的坐标的求法．
练习册系列答案
新编小学单元自测题系列答案
字词句段篇系列答案
相关题目
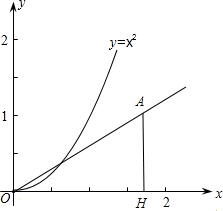如图，在第一象限内作与x轴的夹角为30°的射线OC，在射线OC上取一点A，过点A作AH⊥x轴于点H．在抛物线y=x2（x＞0）上取一点P，在y轴上取一点Q，使得以P，O，Q为顶点的三角形与△AOH全等，则符合条件的点A的坐标是
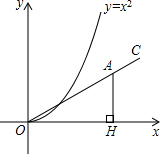如图，在第一象限内作与x轴的夹角为30°的射线OC，在射线OC上取点A，过点A作AH⊥x轴于点H，在抛物线y=x2（x＞0）上取一点P，在y轴上取一点Q，使得P，O，Q为顶点的三角形与△AOH全等，则符合条件的点A有
如图，在第一象限内作射线OC，与x轴的夹角为30°，在射线OC上取一点A，过点A作AH⊥x轴于点H，得到△AOH．在抛物线y=x2（x＞0）上取点P，在y轴上取点Q，使得以P，O，Q为顶点的三角形△POQ与△AOH全等，则符合条件的△AOH的面积是
如图，在第一象限内作射线OC，与x轴的夹角为30°，在射线OC上取点A，过点A作AH⊥x轴于点H．在抛物线y=x2（x＞0）上取点P，在y轴上取点Q，使得以P，O，Q为顶点，且以点Q为直角顶点的三角形与△AOH全等，则符合条件的点A的坐标是