题目内容
以一底角为67.5°的等腰梯形的一腰BC为直径作圆,交大底于E,且恰与另一腰AD相切于M,则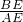 =________.
=________.

分析:连OM,OE,ME,由AD为⊙O的切线,得到OM⊥AD,而四边形ABCD为等腰梯形,且∠ABC=67.5°,则∠OEB=∠OBA=∠A=67.5°,得到OE∥AD,有OE⊥OM,得到△OEM为等腰直角三角形;设OE=R,则ME=
 R,然后证明△OBE∽△MEB,利用相似比即可得到答案.
R,然后证明△OBE∽△MEB,利用相似比即可得到答案.解答:
 解:连OM,OE,ME,如图,
解:连OM,OE,ME,如图,∵AD为⊙O的切线,
∴OM⊥AD,
又∵四边形ABCD为等腰梯形,且∠ABC=67.5°,
而OE=OB,
∴∠OEB=∠OBA=∠A=67.5°,
∴OE∥AD,
∴OE⊥OM,
∴△OEM为等腰直角三角形,
设OE=R,则ME=
 R,
R,又∵∠BOE=180°-67.5°-67.5°=45°,
∠EMA=90°-45°=45°,
∴△OBE∽△MEA,
∴
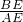 =
=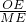 =
=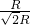 =
= .
.故答案为:
 .
.点评:本题考查了切线的性质:圆心与切点的连线垂直切线;过圆心垂直于切线的直线必过切点;过圆外一点引圆的两条切线,切线长相等.也考查了等腰梯形和切线的性质以及等腰直角三角形的性质.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目

(1)求证:△EOM为等腰直角三角形;
(2)求 的值。
的值。
(2)求
 的值。
的值。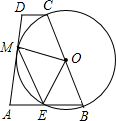 已知:如图,以一底角为67.5°的等腰梯形ABCD的一腰BC为直径做⊙O,交底AB于E,且恰与另一腰AD相切于M;
已知:如图,以一底角为67.5°的等腰梯形ABCD的一腰BC为直径做⊙O,交底AB于E,且恰与另一腰AD相切于M; 已知:如图,以一底角为67.5°的等腰梯形ABCD的一腰BC为直径做⊙O,交底AB于E,且恰与另一腰AD相切于M;
已知:如图,以一底角为67.5°的等腰梯形ABCD的一腰BC为直径做⊙O,交底AB于E,且恰与另一腰AD相切于M; 的值.
的值.
 的值.
的值.