题目内容
 如图,为某食品厂根据通风需要设置的四边形通风调节装置,AB、CD为铁条(宽度不计),O为AB的三等分点、CD的中点,AB=3米,CD=2米,AB可绕O点旋转,阴影部分为遮挡幔布(不通风),空白处可通风,则最大通风面积为
如图,为某食品厂根据通风需要设置的四边形通风调节装置,AB、CD为铁条(宽度不计),O为AB的三等分点、CD的中点,AB=3米,CD=2米,AB可绕O点旋转,阴影部分为遮挡幔布(不通风),空白处可通风,则最大通风面积为
- A.6m2
- B.3m2
- C.1.5m2
- D.无法确定
C
分析:先根据已知条件得出OB=1米,AO=2米,CO=OD=1米,根据等底等高的三角形面积相等得出S△BOC=S△BOD,S△AOD=S△AOC ,再根据四边形的面积公式求出四边形,即可得出答案.
解答:∵O为AB的三等分点、CD的中点,AB=3米,CD=2米,
∴OB=1米,AO=2米,CO=OD=1米,
∴S△BOC=S△BOD,S△AOD=S△AOC,
∵SADBC= AB•CD=
AB•CD=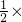 3×2=3(平方米),
3×2=3(平方米),
∴最大通风面积为:3÷2=1.5(平方米);
故选C.
点评:此题考查了三角形的面积公式,解题的关键是掌握三角形的面积公式,等底等高的三角形面积相等.
分析:先根据已知条件得出OB=1米,AO=2米,CO=OD=1米,根据等底等高的三角形面积相等得出S△BOC=S△BOD,S△AOD=S△AOC ,再根据四边形的面积公式求出四边形,即可得出答案.
解答:∵O为AB的三等分点、CD的中点,AB=3米,CD=2米,
∴OB=1米,AO=2米,CO=OD=1米,
∴S△BOC=S△BOD,S△AOD=S△AOC,
∵SADBC=
 AB•CD=
AB•CD=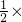 3×2=3(平方米),
3×2=3(平方米),∴最大通风面积为:3÷2=1.5(平方米);
故选C.
点评:此题考查了三角形的面积公式,解题的关键是掌握三角形的面积公式,等底等高的三角形面积相等.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目