题目内容
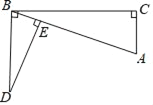
【题目】如图,∠C=∠CBD=90°,DE⊥AB于点E.
(1)求证:△DBE∽△BAC.
(2)若BC=3,DB=2,CA=1,求DE的长.
【答案】(1)详见解析;(2)DE=![]() .
.
【解析】
(1)根据同角的余角相等得出∠D=∠ABC,又∠BED=∠C=90°,根据两角对应相等的两三角形全等即可证明△DBE∽△BAC;(2)在△ABC中,利用勾股定理求出AB=![]() .再根据相似三角形对应边成比例得出
.再根据相似三角形对应边成比例得出![]() ,将数值代入计算即可.
,将数值代入计算即可.
(1)证明:∵∠CBD=90°,DE⊥AB于点E,
∴∠ABC+∠EBD=90°,∠D+∠EBD=90°,
∴∠D=∠ABC.
在△DBE与△BAC中,
![]() ,
,
∴△DBE∽△BAC;
(2)解:在△ABC中,∵∠C=90°,BC=3,CA=1,
∴AB=![]() =
=![]() .
.
由(1)可知,△DBE∽△BAC,
∴![]() ,即
,即![]() =
=![]() ,
,
∴DE=![]() .
.

练习册系列答案
相关题目