题目内容
某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药后2小时时血液中含药量最高,达每毫升6微克(1微克=10-3毫克),接着逐步衰减,10小时时血液中含药量为每毫升3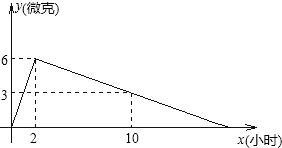 微克,每毫升血液中含药量y(微克),随时间x(小时)的变化如图所示.
微克,每毫升血液中含药量y(微克),随时间x(小时)的变化如图所示.当成人按规定剂量服药后,
(1)分别求出x≤2和x≥2时,y与x之间的函数关系式;
(2)如果每毫升血液中含药量为4微克或4微克以上时在治疗疾病时是有效的,那么这个有效时间是多长?
分析:(1)直接根据图象上的点的坐标利用待定系数法解得
x≤2时,y=3x;
x≥2时,y=-
x+
.
(2)根据图象可知每毫升血液中含药量为4微克是在两个函数图象上都有,所以把y=4,分别代入y=3x,y=-
x+
,解得x1=
,x2=
,所以x2-x1=6小时.
x≤2时,y=3x;
x≥2时,y=-
| 3 |
| 8 |
| 27 |
| 4 |
(2)根据图象可知每毫升血液中含药量为4微克是在两个函数图象上都有,所以把y=4,分别代入y=3x,y=-
| 3 |
| 8 |
| 27 |
| 4 |
| 4 |
| 3 |
| 22 |
| 3 |
解答:解:(1)当x≤2时,设y=k1x,
把(2,6)代入上式,得k1=3,
∴x≤2时,y=3x;
当x≥2时,设y=k2x+b,
把(2,6),(10,3)代入上式,
得k2=-
,b=
.
∴x≥2时,y=-
x+
.
(2)把y=4代入y=3x,得x1=
,
把y=4代入y=-
x+
,得x2=
.
则x2-x1=6小时.
答:这个有效时间为6小时.
把(2,6)代入上式,得k1=3,
∴x≤2时,y=3x;
当x≥2时,设y=k2x+b,
把(2,6),(10,3)代入上式,
得k2=-
| 3 |
| 8 |
| 27 |
| 4 |
∴x≥2时,y=-
| 3 |
| 8 |
| 27 |
| 4 |
(2)把y=4代入y=3x,得x1=
| 4 |
| 3 |
把y=4代入y=-
| 3 |
| 8 |
| 27 |
| 4 |
| 22 |
| 3 |
则x2-x1=6小时.
答:这个有效时间为6小时.
点评:本题主要考查利用一次函数的模型解决实际问题的能力和读图能力.要先根据题意列出函数关系式,再代数求值.解题的关键是要分析题意根据实际意义准确的列出解析式,再把对应值代入求解,并会根据图示得出所需要的信息.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
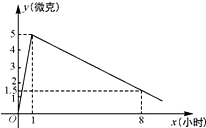 升1.5微克,每毫升血液中含药量y(微克)随时间x(小时)的变化如图所示,在成人按规定剂量服药后:
升1.5微克,每毫升血液中含药量y(微克)随时间x(小时)的变化如图所示,在成人按规定剂量服药后: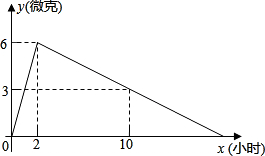 液中含药量为每毫升3微克,每毫升血液中含药量y(微克)随服药后时间x(小时)的变化如图所示,当成人按规定剂量服药后.
液中含药量为每毫升3微克,每毫升血液中含药量y(微克)随服药后时间x(小时)的变化如图所示,当成人按规定剂量服药后.