题目内容
过点P(-1,3)作直线,使它与两坐标轴围成的三角形面积为5,这样的直线可以作条.
- A.4
- B.3
- C.2
- D.1
C
分析:设满足条件的直线L:y=kx+b,因为P(-1,3)在直线上,所以,3=-k+b,故b=k+3,所以y=kx+k+3,可求出与坐标轴的两点,然后根据面积公式可确定k的值从而确定几条直线.
解答:设满足条件的直线L:y=kx+b,因为P(-1,3)在直线上,
所以,3=-k+b,故b=k+3,
所以y=kx+k+3,它与两坐标轴的交点为A(- ,0),B(0,k+3),
,0),B(0,k+3),
S= OA•OB=
OA•OB= |-
|- |•|k+3|=5,
|•|k+3|=5,
(k+3)2=10|k|,
当k>0时,方程k2-4k+9=0无实数解,
当k<0时,方程为k2+16k+9=0,
解得k=-8+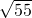 或k=-8-
或k=-8-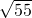 .
.
故选C.
点评:本题考查待定系数法求解析式以及与一元二次方程的结合求解.
分析:设满足条件的直线L:y=kx+b,因为P(-1,3)在直线上,所以,3=-k+b,故b=k+3,所以y=kx+k+3,可求出与坐标轴的两点,然后根据面积公式可确定k的值从而确定几条直线.
解答:设满足条件的直线L:y=kx+b,因为P(-1,3)在直线上,
所以,3=-k+b,故b=k+3,
所以y=kx+k+3,它与两坐标轴的交点为A(-
 ,0),B(0,k+3),
,0),B(0,k+3),S=
 OA•OB=
OA•OB= |-
|- |•|k+3|=5,
|•|k+3|=5,(k+3)2=10|k|,
当k>0时,方程k2-4k+9=0无实数解,
当k<0时,方程为k2+16k+9=0,
解得k=-8+
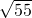 或k=-8-
或k=-8-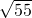 .
.故选C.
点评:本题考查待定系数法求解析式以及与一元二次方程的结合求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
过点P(-1,3)作直线,使它与两坐标轴围成的三角形面积为5,这样的直线可以作( )条.
| A、4 | B、3 | C、2 | D、1 |
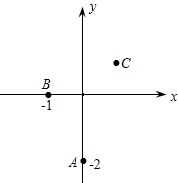 已知二次函数过点A(0,-2),B(-1,0),C(
已知二次函数过点A(0,-2),B(-1,0),C( (2013•田阳县一模)如图,已知直线l:y=
(2013•田阳县一模)如图,已知直线l:y=
