题目内容
直角梯形的中位线为a,一腰长为b,这个腰与底边所成的角为30°,则它的面积为
- A.ab
- B.
 ab
ab - C.
 ab
ab - D.
 ab
ab
B
分析:根据梯形的面积等于梯形的中位线×高,则只需求得梯形的高;根据30°的直角三角形的性质即可求解.
解答:∵一腰长为b,这个腰与底边所成的角为30°,
∴梯形的高为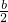 .
.
∴它的面积为 ×2a×
×2a×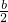 =
= ab.
ab.
故选B.
点评:综合运用了梯形的面积公式以及30°的直角三角形的性质.
分析:根据梯形的面积等于梯形的中位线×高,则只需求得梯形的高;根据30°的直角三角形的性质即可求解.
解答:∵一腰长为b,这个腰与底边所成的角为30°,
∴梯形的高为
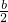 .
.∴它的面积为
 ×2a×
×2a×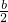 =
= ab.
ab.故选B.
点评:综合运用了梯形的面积公式以及30°的直角三角形的性质.

练习册系列答案
相关题目
直角梯形的中位线为a,一腰长为b,这个腰与底边所成的角为30°,则它的面积为( )
| A、ab | ||
B、
| ||
C、
| ||
D、
|
 ab
ab ab
ab ab
ab ab
ab ab
ab ab
ab