题目内容
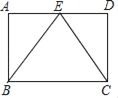
【题目】如图，在矩形ABCD中，点E是边AD的中点，连接BE、CE．
(1)求证：△ABE≌△DCE；
(2)当BC＝2AB，求∠BEC的大小．
【答案】(1)见解析；(2)∠BEC＝90°.
【解析】
（1）根据SAS即可证明；
（2）只要证明△ABE，△DEC都是等腰直角三角形即可解决问题；
(1)证明：∵四边形ABCD是矩形，
∴AB＝DC，∠A＝∠D＝90°.
∵点E是边AD的中点，
∴AE＝DE，∴△ABE≌DCE(SAS)．
(2)∵四边形ABCD是矩形，
∴AD＝BC，∠A＝90°.
∵BC＝2AB，∴AD＝2AB．
∵AD＝2AE，∴AE＝AB，
∴∠AEB＝∠ABE＝45°.
同理可得∠DEC＝45°，
∴∠BEC＝180°－∠AEB－∠DEC＝180°－45°－45°＝90°.
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
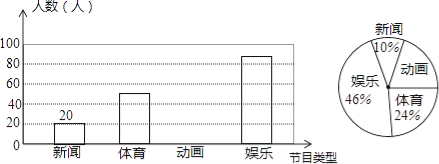
【题目】李晖到“宇泉牌”服装专卖店做社会调查．了解到商店为了激励营业员的工作积极性，实行“月总收入＝基本工资＋计件奖金”的方法，并获得如下信息：
营业员 | 小俐 | 小花 |
月销售件数（件） | 200 | 150 |
月总收入（元） | 1400 | 1250 |
假设月销售件数为
件，月总收入为
元，销售每件奖励
元，营业员月基本工资为
元．
（1）求
的值；
（2）若营业员小俐某月总收入不低于
元，那么小俐当月至少要卖服装多少件？
