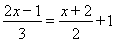题目内容
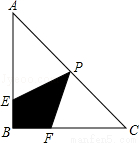
如图,在等腰直角△ABC中,∠ABC=90°,AB=BC=4,P为AC中点,E为AB边上一动点,F为BC边上一动点,且满足条件∠EPF=45°,记四边形PEBF的面积为S1;
(1)求证:∠APE=∠CFP;
(2)记△CPF的面积为S2,CF=x,y=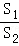 .
.
①求y关于x的函数解析式和自变量的取值范围,并求y的最大值.
②在图中作四边形PEBF关于AC的对称图形,若它们关于点P中心对称,求y的值.
(1)见解析;
(2)①则y关于x的函数解析式为:y=﹣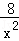 +
+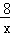 ﹣1,(2≤x≤4),y的最大值为1;
﹣1,(2≤x≤4),y的最大值为1;
②图见解析, y=2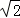 ﹣2.
﹣2.
【解析】
试题分析:(1)分别证出∠APE+∠FPC=∠CFP+∠FPC=135°,即可得出∠APE=∠CFP;
(2)①先证出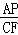 =
=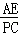 ,再根据AP=CP=2
,再根据AP=CP=2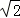 ,得出AE=
,得出AE=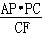 =
= ,过点P作PH⊥AB于点H,PG⊥BC于点G,求出S△APE=
,过点P作PH⊥AB于点H,PG⊥BC于点G,求出S△APE=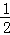 PH•AE=
PH•AE= ,S2=S△PCF=
,S2=S△PCF=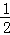 CF×PG=x,再根据S1=S△ABC﹣S△APE﹣S△PCF求出S1=8﹣
CF×PG=x,再根据S1=S△ABC﹣S△APE﹣S△PCF求出S1=8﹣ ﹣x,再代入y=
﹣x,再代入y=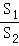 得出y=﹣8(
得出y=﹣8( ﹣
﹣ )2+1,最后根据2≤x≤4,得出
)2+1,最后根据2≤x≤4,得出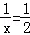 时,y取得最大值,最后将x=2代入y=
时,y取得最大值,最后将x=2代入y=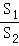 即可求出y最大=1.
即可求出y最大=1.
②根据图中两块阴影部分图形关于点P成中心对称,得出阴影部分图形自身关于直线BD对称,AE=FC,从而得出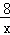 =x,求出x=2
=x,求出x=2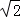 ,最后把
,最后把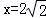 代入y=﹣
代入y=﹣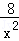 +
+ ﹣1即可.
﹣1即可.
试题解析:(1)∵∠EPF=45°,
∴∠APE+∠FPC=180°﹣45°=135°;
在等腰直角△ABC中,∠PCF=45°,
则∠CFP+∠FPC=180°﹣45°=135°,
∴∠APE=∠CFP.
(2)①∵∠APE=∠CFP,且∠FCP=∠PAE=45°,
∴△APE∽△CFP,
则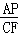 =
=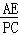 .
.
在等腰直角△ABC中,AC=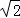 AB=4
AB=4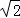 ,
,
又∵P为AC的中点,则AP=CP=2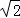 ,
,
∴AE=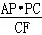 =
=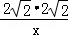 =
=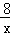 .
.
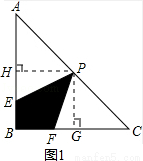
如图1,过点P作PH⊥AB于点H,PG⊥BC于点G,
P为AC中点,则PH∥BC,且PH= BC=2,同理PG=2.
BC=2,同理PG=2.
S△APE= PH•AE=
PH•AE= ×2×
×2×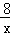 =
=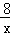 ,
,
S2=S△PCF= CF×PG=
CF×PG= ×x×2=x,
×x×2=x,
∴S1=S△ABC﹣S△APE﹣S△PCF= ×4×4﹣
×4×4﹣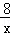 ﹣x=8﹣
﹣x=8﹣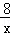 ﹣x,
﹣x,
∴y=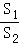 =
= =﹣
=﹣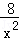 +
+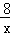 ﹣1=﹣8(
﹣1=﹣8( ﹣
﹣ )2+1,
)2+1,
∵E在AB上运动,F在BC上运动,且∠EPF=45°,
∴2≤x≤4.
即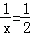 时,y取得最大值.
时,y取得最大值.
而x=2在x的取值范围内,将x=2代入y=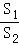 =﹣8(
=﹣8( ﹣
﹣ )2+1,得y最大=1.
)2+1,得y最大=1.
则y关于x的函数解析式为:y=﹣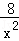 +
+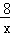 ﹣1,(2≤x≤4),y的最大值为1.
﹣1,(2≤x≤4),y的最大值为1.
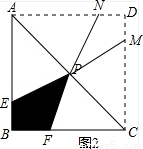
②如图2所示:
图中两块阴影部分图形关于点P成中心对称,则阴影部分图形自身关于直线BD对称,
此时EB=BF,即AE=FC,
则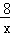 =x,
=x,
解得x1=2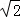 ,x2=﹣2
,x2=﹣2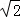 (舍去),
(舍去),
将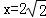 代入y=﹣
代入y=﹣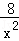 +
+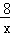 ﹣1,得y=2
﹣1,得y=2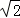 ﹣2.
﹣2.
考点:几何变换综合题.

 口算题天天练系列答案
口算题天天练系列答案