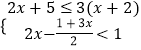题目内容
【题目】综合题
(1)如图1,已知△ABC,点D,E,F分别是BC,AB,AC的中点,若△ABC的面积为16,则△ABD的面积是 , △EBD的面积是 . 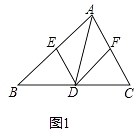
(2)如图2,点D,E,F分别是BC,AD,EC的中点,若△ABC的面积为16,求△BEF的面积是多少?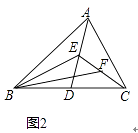
【答案】
(1)8,4
(2)解:∵在△ABC中,D是BC边的中点,
∴S△ABD= ![]() S△ABC=8,
S△ABC=8,
∵E是AD的中点,
∴S△BED= ![]() S△ABD=4,
S△ABD=4,
同理得,S△CDE=4;
∴S△BCE=8,
∵F是CE的中点,
∴S△BEF= ![]() S△BCE=4.
S△BCE=4.
【解析】解:(1)∵点D,E,F分别是BC,AB,AC的中点,三角形中线等分三角形的面积,
∴S△ABD= ![]() S△ABC=
S△ABC= ![]() =8,
=8,
S△EBD= ![]() S△ABD=
S△ABD= ![]() =4,
=4,
所以答案是:8,4;
【考点精析】根据题目的已知条件,利用三角形的面积的相关知识可以得到问题的答案,需要掌握三角形的面积=1/2×底×高.

练习册系列答案
相关题目
【题目】如表记录了一名球员在罚球线上投篮的结果.那么,这名球员投篮一次,投中的概率约为(精确到0.1).
投篮次数(n) | 50 | 100 | 150 | 200 | 250 | 300 | 500 |
投中次数(m) | 28 | 60 | 78 | 104 | 123 | 152 | 251 |
投中频率(m/n) | 0.56 | 0.60 | 0.52 | 0.52 | 0.49 | 0.51 | 0.50 |