题目内容
 如图,已知:在△ABC中,∠A=90°,AB=AC=6,P是AB上不与A、B重合的一动点,PQ⊥BC于Q,QR⊥AC于R.
如图,已知:在△ABC中,∠A=90°,AB=AC=6,P是AB上不与A、B重合的一动点,PQ⊥BC于Q,QR⊥AC于R.(1)求证:PQ=BQ;
(2)设BP的长为x,QR的长为y,求y与x之间的函数关系式,并写出函数的定义域;
(3)PR能否平行于BC?如果能,试求出x的值;若不能,请简述理由.
分析:(1)若证明PQ=BQ,则问题可转化为证明∠B=∠BPQ即可,
(2)利用勾股定理得到BQ和PQ的长,又因为BQ2+PQ2=BP2,BP=x,把BQ和PQ代入等式化简即可得到y与x之间的函数关系式,
(3)PR能平行于BC,只要证明AP=AR,即可求出x的值.
(2)利用勾股定理得到BQ和PQ的长,又因为BQ2+PQ2=BP2,BP=x,把BQ和PQ代入等式化简即可得到y与x之间的函数关系式,
(3)PR能平行于BC,只要证明AP=AR,即可求出x的值.
解答:(1)证明:∵∠A=90°,AB=AC=6,
∴∠B=∠C=45°,BC=
=6
,
∵PQ⊥BC,
∴∠PQB=90°,
∴∠BPQ=45°,
∴∠B=∠BPQ,
∴PQ=BQ;
(2)∵QR⊥AC,
∴∠QRC=90°,
∵∠C=45°,
∴∠RQC=45°,
∴∠C=∠RQC,
∴RQ=RC=y,
∴QC=
y,
∴BQ=6
-
y,
∴PQ=6
-
y,
∵BQ2+PQ2=BP2,BP=x,
∴(6
-
y)2+(6
-
y)2=x2,
∴y=6-
(0<x<6);
(3)PR能平行于BC.
理由如下:
∵PR∥BC,
∴∠APR=∠ARP,
∴AP=AR,
∴6-x=6-y6-x=6-(6-
),
∴x=4.
∴∠B=∠C=45°,BC=
| 62+62 |
| 2 |
∵PQ⊥BC,
∴∠PQB=90°,
∴∠BPQ=45°,
∴∠B=∠BPQ,
∴PQ=BQ;
(2)∵QR⊥AC,
∴∠QRC=90°,
∵∠C=45°,
∴∠RQC=45°,
∴∠C=∠RQC,
∴RQ=RC=y,
∴QC=
| 2 |
∴BQ=6
| 2 |
| 2 |
∴PQ=6
| 2 |
| 2 |
∵BQ2+PQ2=BP2,BP=x,
∴(6
| 2 |
| 2 |
| 2 |
| 2 |
∴y=6-
| x |
| 2 |
(3)PR能平行于BC.
理由如下:
∵PR∥BC,
∴∠APR=∠ARP,
∴AP=AR,
∴6-x=6-y6-x=6-(6-
| x |
| 2 |
∴x=4.
点评:本题考查了勾股定理的运用、等腰三角形的判定和性质、平行线的判定和性质以及列函数关系式,题目的难度中等.

练习册系列答案
相关题目

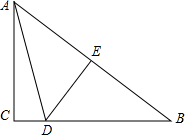 如图,已知:在Rt△ABC中,∠C=90°,E为AB的中点,且DE⊥AB于E,若∠CAD:∠DAB=1﹕2,求∠B的度数.
如图,已知:在Rt△ABC中,∠C=90°,E为AB的中点,且DE⊥AB于E,若∠CAD:∠DAB=1﹕2,求∠B的度数.