Question

已知线段AB₁=2，顺次做线段B₁B₂⊥AB₁，B₁B₂=1，连AB₂；线段B₂B₃⊥AB₂，B₂B₃=1，连AB₃；…；线段B_n-1B_n⊥AB_n，B_n-1B_n=1，连AB_n；若AB_n=10，则n=

97

．

Answer 1

分析：根据题意画出图形，在Rt△AB₁B₂中，由B₁B₂及AB₁的长，利用勾股定理得AB₂的长；在Rt△AB₂B₃中，由B₂B₃及AB₂的长，利用勾股定理得AB₃的长；在Rt△AB₃B₄中，由B₃B₄及AB₃，的长，利用勾股定理得AB₄的长；…；依此类推，按照此规律得到AB_n=

n+3

，由已知的AB_n=10，两者相等即可求出此时n的值．

解答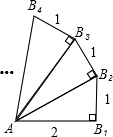：解：根据题意画出图形，如图所示：
在Rt△AB₁B₂中，B₁B₂=1，AB₁=2，
根据勾股定理得：AB₂=

12+22

=

5

；
在Rt△AB₂B₃中，B₂B₃=1，AB₂=

5

，
根据勾股定理得：AB₃=

12+( 5 )2

=

6

；
在Rt△AB₃B₄中，B₃B₄=1，AB₃=

6

，
根据勾股定理得：AB₄=

12+( 6 )2

=

7

；
…，
∴AB_n=

n+3

，
若AB_n=10，则有

n+3

=10，
解得n=97．
故答案为：97

点评：此题考查了勾股定理的应用，锻炼了学生概括、归纳、总结的能力，根据题意画出相应的图形，根据图形，多次利用勾股定理，分别求出AB₂，AB₃，AB₃，以及AB₄的长，观察B右下角数字与结果中被开方数的关系，得出一般性的结论是解本题的关键．