题目内容
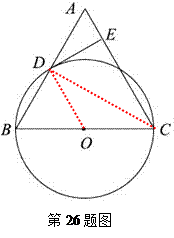
（2011贵州安顺，26，12分）已知：如图，在△ABC中，BC=AC，以BC为直径的⊙O与边AB相交于点D，DE⊥AC，垂足为点E．⑴求证：点D是AB的中点；
⑵判断DE与⊙O的位置关系，并证明你的结论；
⑶若⊙O的直径为18，cosB =
，求DE的长．
（1）证明：连接CD,则CD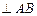
， 又∵AC = BC， CD = CD， ∴
≌
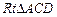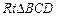
∴AD = BD， 即点D是AB的中点．
（2）DE是⊙O的切线 ．
理由是：连接OD, 则DO是△ABC的中位线，∴DO∥AC， 又∵DE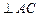
；
∴DE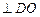
即DE是⊙O的切线；
（3）∵AC = BC， ∴∠B =∠A， ∴cos∠B = cos∠A =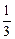
， ∵cos∠B =
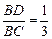， BC = 18，
∴BD =" 6" ， ∴AD =" 6" ， ∵cos∠A =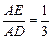
， ∴AE = 2，
在
中，DE=
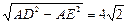．解析:
略
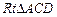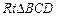
， 又∵AC = BC， CD = CD， ∴≌∴AD = BD， 即点D是AB的中点．
（2）DE是⊙O的切线 ．
理由是：连接OD, 则DO是△ABC的中位线，∴DO∥AC， 又∵DE
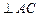；∴DE
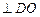即DE是⊙O的切线；（3）∵AC = BC， ∴∠B =∠A， ∴cos∠B = cos∠A =
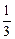， ∵cos∠B =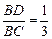， BC = 18，∴BD =" 6" ， ∴AD =" 6" ， ∵cos∠A =
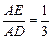， ∴AE = 2，在
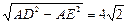中，DE=．解析:略
练习册系列答案
开心蛙口算题卡系列答案
相关题目
，其中a=2－
