题目内容
等边三角形两条角平分线所夹锐角的度数是
- A.120°
- B.150°
- C.60°
- D.90°
C
试题分析:根据已知条件和等边三角形的性质可知:∠1=∠2=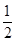 ∠ABC=30°,所以∠3=∠1+∠2=60°.
∠ABC=30°,所以∠3=∠1+∠2=60°.
如图,

∵等边三角形ABC中,AD,BE分别是∠BAC,∠ABC的角的平分线,交于点F,
∴∠1=∠2=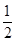 ∠ABC=30°(角平分线的定义和等边三角形的性质),
∠ABC=30°(角平分线的定义和等边三角形的性质),
∴∠3=∠1+∠2=60°(三角形的一个外角等于与它不相邻的两个内角的和).
故选C.
考点:本题考查的是等边三角形的性质
点评:解答本题的关键是掌握等边三角形的三角均为60°,三角形的一个外角等于与它不相邻的两个内角的和.
试题分析:根据已知条件和等边三角形的性质可知:∠1=∠2=
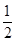 ∠ABC=30°,所以∠3=∠1+∠2=60°.
∠ABC=30°,所以∠3=∠1+∠2=60°.如图,

∵等边三角形ABC中,AD,BE分别是∠BAC,∠ABC的角的平分线,交于点F,
∴∠1=∠2=
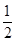 ∠ABC=30°(角平分线的定义和等边三角形的性质),
∠ABC=30°(角平分线的定义和等边三角形的性质),∴∠3=∠1+∠2=60°(三角形的一个外角等于与它不相邻的两个内角的和).
故选C.
考点:本题考查的是等边三角形的性质
点评:解答本题的关键是掌握等边三角形的三角均为60°,三角形的一个外角等于与它不相邻的两个内角的和.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目