Question

【题目】如图所示，∠E=∠F=90°，∠B=∠C，AE=AF．给出下列结论：①∠1=∠2；②BE=CF；
③△ACN≌△ABM；④CD=DN．其中正确的是（将正确的结论的序号都填上）．

Answer 1

【答案】①②③
【解析】解：在ABE和ACF中，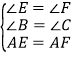
，
∴ABEACF（AAS）
∴BAE=CAF，AC=AB，BE=CF（即②正确），
∴BAE-BAC=CAF-BAC，
即1=2. （即①正确）.
在ACN和ABM中，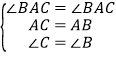
,
∴ACNABM（ASA）（即③正确）.
∴AN=AM，
∴AB-AN=AC-AM，
即BN=CM.
在CDM和BDN中，
，
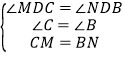∴CDMBDN（AAS），
∴CD=BD.
对于④，假设CD=DN成立，由CD=BD知DN=BD，则DNB=B，又∵∠B=∠C，
∴DNB=∠C，
∴ACAB，而题中AC与AB相交于点A，与已知矛盾.
∴假设不成立，即CDDN.（即④错误）.
综上，题中正确的结论是①②③.
故答案是：①②③.