Question

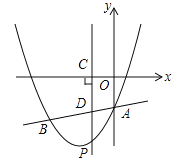
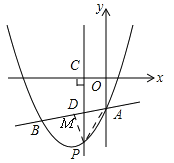
【题目】如图，抛物线与直线交于A、B两点，其中点A在y轴上，点B坐标为（﹣4，﹣5），点P为y轴左侧的抛物线上一动点，过点P作PC⊥x轴于点C，交AB于点D．

（1）求抛物线的解析式；

（2）以O，A，P，D为顶点的平行四边形是否存在？如存在，求点P的坐标；若不存在，说明理由．

（3）当点P运动到直线AB下方某一处时，过点P作PM⊥AB，垂足为M，连接PA使△PAM为等腰直角三角形，请直接写出此时点P的坐标．

Answer 1

【答案】（1）；（2）P（，），（﹣1，），（﹣3，）；（3）P（，）．

【解析】

试题分析：（1）先确定出点A坐标，然后用待定系数法求抛物线解析式；

（2）先用m表示出PD，当PD=OA=3，故存在以O，A，P，D为顶点的平行四边形，得到，分两种情况进行讨论计算即可；

（3）由△PAM为等腰直角三角形，得到∠BAP=45°，从而求出直线AP的解析式，最后求出直线AP和抛物线的交点坐标即可．

试题解析：（1）∵直线交于A、B两点，其中点A在y轴上，∴A（0，﹣3），∵B（﹣4，﹣5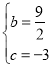），∴，∴，∴抛物线解析式为；

（2）存在，设P（m，），（m＜0），∴D（m，），∴PD=．

∵PD∥AO，∴当PD=OA=3，故存在以O，A，P，D为顶点的平行四边形，∴；

①当时，∴=，=（舍），∴=，∴P（，）；

②当时，∴=﹣1，=﹣3．

Ⅰ、m1=﹣1，∴=，∴P（﹣1，）；

Ⅱ、m2=﹣3，∴=，∴P（﹣3，）；

∴点P的坐标为（，），（﹣1，），（﹣3，）；

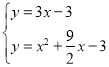（3）如图，∵△PAM为等腰直角三角形，∴∠BAP=45°，∵直线AP可以看做是直线AB绕点A逆时针旋转45°所得，设直线AP解析式为y=kx﹣3，∵直线AB解析式为，∴k==3，∴直线AP解析式为y=3x﹣3，联立：，∴=0（舍），=；

当x=时，y=，∴P（，）．