��Ŀ����
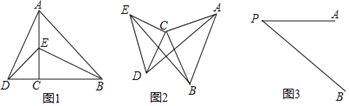
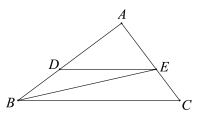
����Ŀ����ͼ������ABC�У�AB=5��AC=9��S��ABC=![]() ������P��A�������������AB������ÿ��5����λ���ٶ��˶�������Q��C�����������ͬ���ٶ����߶�AC����C��A�˶�����Q���˶���A��ʱ��P��Q����ͬʱֹͣ�˶�����PQΪ����������PQEF��P��Q��E��F����ʱ��������CQΪ����AC�Ϸ���������QCGH��
������P��A�������������AB������ÿ��5����λ���ٶ��˶�������Q��C�����������ͬ���ٶ����߶�AC����C��A�˶�����Q���˶���A��ʱ��P��Q����ͬʱֹͣ�˶�����PQΪ����������PQEF��P��Q��E��F����ʱ��������CQΪ����AC�Ϸ���������QCGH��
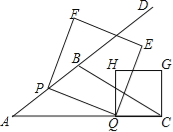
��1����tanA��ֵ��
��2�����P�˶�ʱ��Ϊt��������PQEF�����ΪS����̽��S�Ƿ������Сֵ�������ڣ���������Сֵ���������ڣ���˵�����ɣ�
��3����tΪ��ֵʱ��������PQEF��ij�����㣨Q����⣩����������QCGH�ı��ϣ���ֱ��д��t��ֵ��
���𰸡���1��![]() ����2�����ڣ�S��Сֵ=
����2�����ڣ�S��Сֵ=![]() ����3��t1=
����3��t1=![]() ��t2=
��t2=![]() ��t3=1��t4=
��t3=1��t4=![]() ��
��
��������
���⣨1����ͼ1������B��BM��AC�ڵ�M��������������BM�ij��ȣ����ù��ɶ����õ�AM�ij��ȣ������������Ǻ����Ķ�����н��
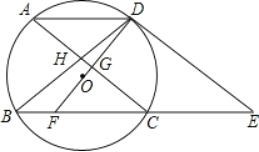
��2����ͼ2������P��PN��AC�ڵ�N�����ã�1���еĽ��ۺ��ɶ����õ�PN2+NQ2=PQ2�������������ε������ʽ�õ�S����t�Ķ��κ��������ö��κ����Ķ������깫ʽ�Ͷ��κ���ͼ���������������ֵ��
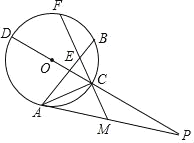
��3����Ҫ�������ۣ�����E�ڱ�HG�ϡ���F�ڱ�HG�ϡ���P��QH�����E��QC�ϣ�����F��C��ʱ���Ӧ��t��ֵ��
����������⣺��1����ͼ1������B��BM��AC�ڵ�M��
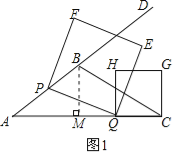
��AC=9��S��ABC=![]() ��
��
��![]() ACBM=
ACBM=![]() ����
����![]() ��9BM=
��9BM=![]() ��
��
���BM=3��
�ɹ��ɶ�������
AM=![]() =
=![]() =4��
=4��
��tanA=![]() =
=![]() ��
��
��2�����ڣ�
��ͼ2������P��PN��AC�ڵ�N��

�������AP=CQ=5t��
��tanA=![]() ��
��
��AN=4t��PN=3t��
��QN=AC��AN��CQ=9��9t��
���ݹ��ɶ����õ���PN2+NQ2=PQ2��
S������PQEF=PQ2=��3t��2+��9��9t��2=90t2��162t+81��0��t��![]() ����
����
�ߩ�/span>![]() =
=![]() =
=![]() ��t��ȡֵ��Χ֮�ڣ�
��t��ȡֵ��Χ֮�ڣ�
��S��Сֵ=![]() =
=![]() =
=![]() ��
��
��3��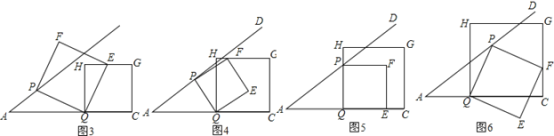
����ͼ3������E�ڱ�HG��ʱ��t1=![]() ��
��
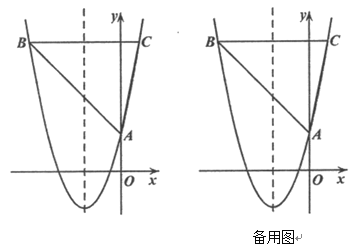
����ͼ4������F�ڱ�HG��ʱ��t2=![]() ��
��
����ͼ5������P��QH�����E��QC�ϣ�ʱ��t3=1
����ͼ6������F��C��ʱ��t4=![]() ��
��

����Ŀ��������Ϊ���˽���꼶450��ѧ����������������������˾��꼶����ѧ���������������ԣ���λ�����������ݲ��Խ�����Ƴ������治������ͳ��ͼ����
��� | ������ | Ƶ�� | Ƶ�� |
1 |
| 5 | 0.1 |
2 |
| 21 | 0.42 |
3 |
|
| |
4 |
|
|
��1�������![]() �� ����
�� ����![]() �� ����
�� ����
��2������þ��꼶���������Խ��С��10��������
��3�����������Խ��С��10��Ϊ����꣬��������5������3��������2��Ů�����ִ���5�������ѡ��2�˵��飬��ͨ������״ͼ���б��ķ�����ѡ����2��Ϊһ������һ��Ů���ĸ��ʣ�