题目内容
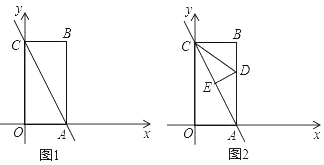
【题目】如图1，在平面直角坐标系中，一次函数
的图象与
轴，
轴分别交于点
，点
，过点作
轴，垂足为点，过点作
轴，垂足为点，两条垂线相交于点
．
（1）线段
，
，
的长分别为
_______，
_________，
_________；
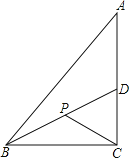
（2）折叠图1中的
，使点与点重合，再将折叠后的图形展开，折痕
交于点
，交于点
，连接
，如图2．
①求线段
的长；
②在轴上，是否存在点
，使得
为等腰三角形？若存在，请直接写出符合条件的所有点的坐标；若不存在，请说明理由．
【答案】（1）8；4；
；（2）①线段AD的长为5；②点P的坐标为（0，3）或（0，-3）或（0，2）或（0，8）或（0，
）．
【解析】
（1）利用一次函数图象上点的坐标特征可求出点A，C的坐标，利用矩形的性质及勾股定理，可得出AB，BC，AC的长；
（2）①设AD=a，则CD=a，BD=8-a，在Rt△BCD中，利用勾股定理可求出a的值，进而可得出线段AD的长；
②设点P的坐标为（0，t），利用两点间的距离公式可求出AD2，AP2，DP2的值，分AP=AD，AD=DP及AP=DP三种情况，可得出关于t的一元二次方程（或一元一次方程），解之即可得出t的值，进而可得出点P的坐标．
解：（1）如图：
当x=0时，y=-2x+8=8，
∴点C的坐标为（0，8）；
当y=0时，-2x+8=0，解得：x=4，
∴点A的坐标为（4，0）．
由已知可得：四边形OABC为矩形，
∴AB=OC=8，BC=OA=4，AC=
．
故答案为：8；4；．
（2）①设AD=a，则CD=a，BD=8-a．
在Rt△BCD中，CD2=BC2+BD2，即a2=42+（8-a）2，
解得：a=5，
∴线段AD的长为5．
②存在，如图：
设点P的坐标为（0，t）．
∵点A的坐标为（4，0），点D的坐标为（4，5），
∴AD2=25，AP2=（0-4）2+（t-0）2=t2+16，DP2=（0-4）2+（t-5）2=t2-10t+41．
当AP=AD时，t2+16=25，
解得：t=±3，
∴点P的坐标为（0，3）或（0，-3）；
当AD=DP时，25=t2-10t+41，
解得：t1=2，t2=8，
∴点P的坐标为（0，2）或（0，8）；
当AP=DP时，t2+16=t2-10t+41，
解得：t=，
∴点P的坐标为（0，）．
综上所述：在y轴上存在点P，使得△APD为等腰三角形，点P的坐标为（0，3）或（0，-3）或（0，2）或（0，8）或（0，）．
【题目】如图，抛物线y=x2-2x-3与x轴交于A、B两点，与y轴交于点C.
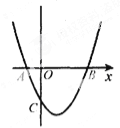
（1）点A的坐标为 点B的坐标为 ，点C的坐标为 ；
（2）设抛物线y=x2-2x-3的顶点坐标为M，求四边形ABMC的面积.
【题目】如图，一个滑道由滑坡（AB段）和缓冲带（BC段）组成，滑雪者在滑坡上滑行的距离y1（单位：m）和滑行时间t1（单位s）满足二次函数关系，并测得相关数据：
滑行时间t1/s | 0 | 1 | 2 | 3 | 4 |
滑行距离y1/s | 0 | 4.5 | 14 | 28.5 | 48 |
滑雪者在缓冲带上滑行的距离y2（单位：m）和滑行时间t2（单位：s）满足：y2=52t2﹣2t22，滑雪者从A出发在缓冲带BC上停止，一共用了23s．
（1）求y1和t1满足的二次函数解析式；
（2）求滑坡AB的长度．
