题目内容
【题目】(1) 发现：
如图1，点
是线段
外一动点，且
，
．当点位于 时，线段
的长取得最大值；最大值为 (用含
，
的式子表示)．
(2)应用：
如图2，点为线段外一动点，
，
，分别以
，为边在
外部作等边
和等边
，连接
，
．
①求证：
；
②直接写出线段长的最大值．
(3)拓展：
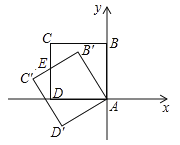
如图3，在平面直角坐标系中，点
，点
，点
为线段外一动点，
，
，
，请直接写出线段
长的最大值及此时点的坐标．
【答案】（1）线段
的延长线上，
；（2）①证明见解析；②3；③
，（2-
，）或（2-，-）．
【解析】
（1）根据点A位于CB的延长线上时，线段AC的长取得最大值，即可得到结论；
（2）①根据等边三角形的性质得到AD=AB，AC=AE，∠BAD=∠CAE=60°，推出△CAD≌△EAB，根据全等三角形的性质得到CD=BE；②由于线段BE长的最大值=线段CD的最大值，根据（1）中的结论即可得到结果；
（3）连接BM，将△APM绕着点P顺时针旋转90°得到△PBN，连接AN，得到△APN是等腰直角三角形，根据全等三角形的性质得到PN=PA=2，BN=AM，根据当N在线段BA的延长线时，线段BN取得最大值，即可得到最大值为
；如图2，过P作PE⊥x轴于E，根据等腰直角三角形的性质即可得到结论．
（1）∵点A为线段BC外一动点，且BC=a，AB=b，
∴当点A位于CB的延长线上时，线段AC的长取得最大值，且最大值为BC+AB=a+b，
故答案为：CB的延长线上，a+b；
（2）①证明: ∵
是等边三角形.
∴
，
，
∵
是等边三角形，
∴
， 
，
∴
，
∴
，
∴
.
在
与
中，
∴
（
），
∴
.即
.
②∵线段BE长的最大值=线段CD的最大值，
由（1）知，当线段CD的长取得最大值时，点D在CB的延长线上，
∴最大值为BD+BC=AB+BC=3；.
（3）如图1，
∵将△APM绕着点P顺时针旋转90°得到△PBN，连接AN，
则△APN是等腰直角三角形，
∴PN=PA=3，BN=AM，
∵A的坐标为（3，0），点B的坐标为（5，0），
∴OA=3，OB=5，
∴AB=2，
∴线段AM长的最大值=线段BN长的最大值，
∴当N在线段BA的延长线上时，线段BN取得最大值，
最大值=AB+AN，
∵AN=
AP=3，
∴最大值为3+2；
如图2，
过P作PE⊥x轴于E，
∵△APN是等腰直角三角形，
∴PE=AE=，
∴OE=BO-AB-AE=5-3-=2-，
∴P（2-，）．
如图3中，
根据对称性可知当点P在第四象限时，P（2-，-）时，也满足条件．
综上所述，满足条件的点P坐标（2-，）或（2-，-），AM的最大值为3+2．
