题目内容
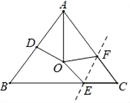
【题目】如图，∠BAC＝30°，AM是∠BAC的平分线，过M作ME∥BA交AC于E，作MD⊥BA，垂足为D，ME＝10cm，则MD＝_________.
【答案】5cm
【解析】
如图，过M作MF⊥AC于F，先根据角平分线的性质得出MD=MF，再由平行线的性质得出∠FEM=∠BAC=30°，从而在Rt△MEF中，利用30°角所对的直角边等于斜边的一半，得出MF=
ME ，根据MD=MF即可求出MD的长.
过M作MF⊥AC于F，
∵AM是∠BAC的平分线，MF⊥AC，MD⊥BA，
∴MD=MF
∵EM//AB
∴∠FEM=∠BAC=30°，
∵在直角三角形EMF中，∠FEM=30°，EM为斜边，
∴MF=EM=5cm，
∴MD=MF=5
故答案为：5cm
练习册系列答案
相关题目
【题目】为了解某种品牌小汽车的耗油量，我们对这种车在高速公路上做了耗油试验，并把试验的数据记录下来，制成下表：
汽车行驶时间t（h） | 0 | 1 | 2 | 3 | … |
油箱剩余油量Q（L） | 100 | 94 | 88 | 82 | … |
①根据上表的数据，请你写出Q与t的关系式；
②汽车行驶5h后，油箱中的剩余油量是多少？
③该品牌汽车的油箱加满50L，若以100km/h的速度匀速行驶，该车最多能行驶多远？