题目内容
如图,王明站在地面B处用测角仪器测得楼顶点E的仰角为45°,楼顶上旗杆顶点F的仰角为55°,已知测角仪器高AB=1.5米,楼高CE=14.5米,求旗杆EF的高度(精确到1米).(供参考数据:sin55°≈0.8,cos55°≈0.57,tan55°≈1.4).
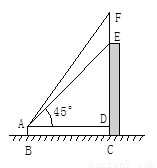
【答案】
旗杆EF的高约为5米
【解析】
试题分析:易知四边形ABCD为矩形,CD=AB=1.5米,
∴DE=CE-AB=13.
在Rt△ADE中,∵∠EAD=45°,
AD=DE=13米,
在Rt△ADF中,∠FAD=55°,
DF=AD·tan55°=13×1.4=18.2,
∴EF=DF-DE=18.2-13=5.2≈5(米).
答:旗杆EF的高约为5米.
考点:三角函数
点评:本题考查三角函数,解答本题要求考生掌握三角函数的定义,利用三角函数的定义来做题,要求考生会做有关三角函数的题

练习册系列答案
相关题目
 20、如图,王明站在地面B处用测角仪器测得楼顶点E的仰角为45°,楼顶上旗杆顶点F的仰角为55°,已知测角仪器高AB=1.5米,楼高CE=14.5米,求旗杆EF的高度(精确到1米).(供参考数据:sin55°≈0.8,cos55°≈0.57,tan55°≈1.4.)
20、如图,王明站在地面B处用测角仪器测得楼顶点E的仰角为45°,楼顶上旗杆顶点F的仰角为55°,已知测角仪器高AB=1.5米,楼高CE=14.5米,求旗杆EF的高度(精确到1米).(供参考数据:sin55°≈0.8,cos55°≈0.57,tan55°≈1.4.)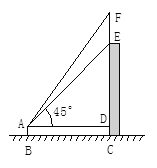
 如图,王明站在地面B处用测角仪器测得楼顶点E的仰角为45°,楼顶上旗杆顶点F的仰角为55°,已知测角仪器高AB=1.5米,楼高CE=14.5米,求旗杆EF的高度(精确到1米).(供参考数据:sin55°≈0.8,cos55°≈0.57,tan55°≈1.4.)
如图,王明站在地面B处用测角仪器测得楼顶点E的仰角为45°,楼顶上旗杆顶点F的仰角为55°,已知测角仪器高AB=1.5米,楼高CE=14.5米,求旗杆EF的高度(精确到1米).(供参考数据:sin55°≈0.8,cos55°≈0.57,tan55°≈1.4.)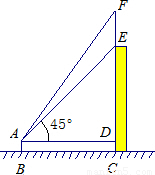 如图,王明站在地面B处用测角仪器测得楼顶点E的仰角为45°,楼顶上旗杆顶点F的仰角为55°,已知测角仪器高AB=1.5米,楼高CE=14.5米,求旗杆EF的高度(精确到1米).(供参考数据:sin55°≈0.8,cos55°≈0.57,tan55°≈1.4.)
如图,王明站在地面B处用测角仪器测得楼顶点E的仰角为45°,楼顶上旗杆顶点F的仰角为55°,已知测角仪器高AB=1.5米,楼高CE=14.5米,求旗杆EF的高度(精确到1米).(供参考数据:sin55°≈0.8,cos55°≈0.57,tan55°≈1.4.)