Question

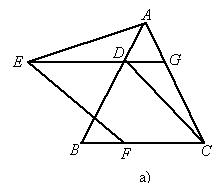
(2005·四川成都)已知：如图a所示，△ABC是等边三角形，过AB边上的点D作DG∥BC，交AC于点G，在GD的延长线上取点E，使DE=DB，连接AE、CD．

(1)求证：△AGE≌△DAC；

(2)过点E作EF∥DC，交BC于点F，请你连接AF，并判断△AEF是怎样的三角形，并证明你的结论．

Answer 1

答案：略
解析：

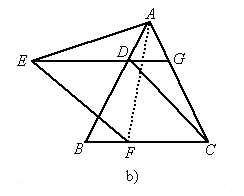
证明　(1)∵如图所示，△ABC是等边三角形． 　　∴AB=AC=BC，∠BAC=∠ABC=∠ACB=60°． 　　∵EG∥BC，∴∠ADG=∠ABC=60°， 　　∠AGD=∠ACB=60°． 　　∴△ADG是等边三角形． 　　∴AD=DG=AG 　　∵DE=DB，∴EG=AB．∴GE=AC 　　∴在△AGE和△DAC中， 　　∵EG=AB=CA， 　　∠AGE=∠DAC=60°，AG=DA， 　　∴△ACE≌△DAC． (2)如图b所示 连接AF，则△AEF是等边三角形． 　　∵EG∥BC，EF∥DC， 　　∴四边形EFCD是平行四边形． 　　∴EF=DC，∠DEF=∠DCF． 　　∵△AGE≌△DAC， 　　∴∠AE=CD，∠AED=∠ACD． 　　∵EF=CD=AE，∠AED＋∠DEF= ∠ACD＋∠DCB=60°， 　　∴△AEF是等边三角形．