题目内容
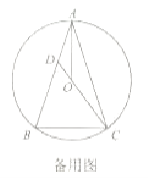
【题目】已知:如图,△ABC中,∠A=90°,BC的垂直平分线DE交BC于点E,交AC于点D.
(1)若∠C=35°,求∠DBA的度数;
(2)若△ABD的周长为30,AC=18,求AB的长.
【答案】
(1)解:∵DE是BC的垂直平分线,
∴CD=BD,
∴∠CBD=∠C=35°,
∴∠ADB=∠C+∠CBD=70°,
∵△ABC中,∠A=90°,
∴∠DBA=90°﹣∠BDA=20°;
(2)解:∵△ABD的周长为30,CD=BD,
∴AB+AD+BD=AB+AD+CD=AB+AC=30,
∵AC=18,
∴AB=30﹣18=12.
【解析】(1)抓住题中关键的已知条件BC的垂直平分线DE,得出CD=BD,可求出∠CBD、∠C的度数,再根据直角三角形两锐角互余,求出∠ABC的度数,即可求得∠DBA的度数。
(2)由(1)的证明过程可知,CD=BD,因此△ABD的周长=AC+AB=30,即可求出AB的长。
【考点精析】本题主要考查了三角形的内角和外角和线段垂直平分线的性质的相关知识点,需要掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等才能正确解答此题.

 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案【题目】某公司共有![]() 三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图.
三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图.

各部门人数及每人所创年利润统计表
部门 | 员工人数 | 每人所创的年利润/万元 |
A | 5 | 10 |
B |
| 8 |
C |
| 5 |
(1)①在扇形图中,C部门所对应的圆心角的度数为___________;
②在统计表中,![]() ___________,
___________,![]() ___________;
___________;
(2)求这个公司平均每人所创年利润.