题目内容
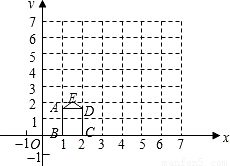 (2008•陕西)如图,矩形ABCD的长,宽分别为
(2008•陕西)如图,矩形ABCD的长,宽分别为 和1,且OB=1,点E(
和1,且OB=1,点E( ,2),连接AE,ED.
,2),连接AE,ED.(1)求经过A,E,D三点的抛物线的表达式;
(2)若以原点为位似中心,将五边形AEDCB放大,使放大后的五边形的边长是原五边形对应边长的3倍,请在下图网格中画出放大后的五边形A′E′D′C′B′;
(3)经过A′,E′,D′三点的抛物线能否由(1)中的抛物线平移得到?请说明理由.
【答案】分析:(1)A,E,D三点坐标已知,可用一般式来求解;
(2)延长OA到A′,使OA′=3OA,同理可得到其余各点;
(3)根据二次项系数是否相同即可判断两个函数是否由平移得到.
解答: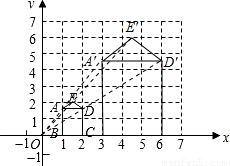 解:(1)设经过A,E,D三点的抛物线的表达式为y=ax2+bx+c
解:(1)设经过A,E,D三点的抛物线的表达式为y=ax2+bx+c
∵A(1, ),E(
),E( ,2),D(2,
,2),D(2, )(1分)
)(1分)
∴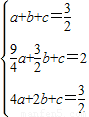 ,解之,得
,解之,得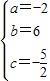
∴过A,E,D三点的抛物线的表达式为y=-2x2+6x- .(4分)
.(4分)
(2)如图.(7分)
(3)不能,理由如下:(8分)
设经过A′,E′,D′三点的抛物线的表达式为y=a′x2+b′x+c′
∵A′(3, ),E′(
),E′( ,6),D′(6,
,6),D′(6, )
)
∴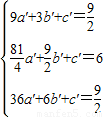 ,
,
解之,得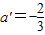
a=-2,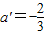 ,
,
∴a≠a′
∴经过A′,E′,D′三点的抛物线不能由(1)中的抛物线平移得到.(8分)
点评:一般用待定系数法来求函数解析式;位似变化的方法应熟练掌握;抛物线平移不改变a的值.
(2)延长OA到A′,使OA′=3OA,同理可得到其余各点;
(3)根据二次项系数是否相同即可判断两个函数是否由平移得到.
解答:
 解:(1)设经过A,E,D三点的抛物线的表达式为y=ax2+bx+c
解:(1)设经过A,E,D三点的抛物线的表达式为y=ax2+bx+c∵A(1,
 ),E(
),E( ,2),D(2,
,2),D(2, )(1分)
)(1分)∴
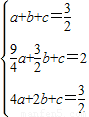 ,解之,得
,解之,得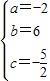
∴过A,E,D三点的抛物线的表达式为y=-2x2+6x-
 .(4分)
.(4分)(2)如图.(7分)
(3)不能,理由如下:(8分)
设经过A′,E′,D′三点的抛物线的表达式为y=a′x2+b′x+c′
∵A′(3,
 ),E′(
),E′( ,6),D′(6,
,6),D′(6, )
)∴
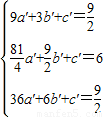 ,
,解之,得
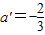
a=-2,
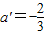 ,
,∴a≠a′
∴经过A′,E′,D′三点的抛物线不能由(1)中的抛物线平移得到.(8分)
点评:一般用待定系数法来求函数解析式;位似变化的方法应熟练掌握;抛物线平移不改变a的值.

练习册系列答案
相关题目
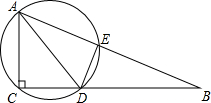 (2008•陕西)如图,在Rt△ABC中,∠ACB=90°,AC=5,CB=12,AD是△ABC的角平分线,过A、C、D三点的圆O与斜边AB交于点E,连接DE.
(2008•陕西)如图,在Rt△ABC中,∠ACB=90°,AC=5,CB=12,AD是△ABC的角平分线,过A、C、D三点的圆O与斜边AB交于点E,连接DE.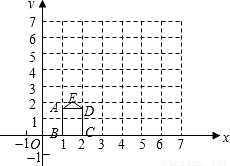 (2008•陕西)如图,矩形ABCD的长,宽分别为
(2008•陕西)如图,矩形ABCD的长,宽分别为 和1,且OB=1,点E(
和1,且OB=1,点E( ,2),连接AE,ED.
,2),连接AE,ED.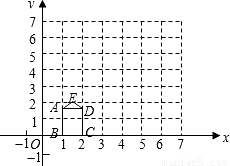 (2008•陕西)如图,矩形ABCD的长,宽分别为
(2008•陕西)如图,矩形ABCD的长,宽分别为 和1,且OB=1,点E(
和1,且OB=1,点E( ,2),连接AE,ED.
,2),连接AE,ED.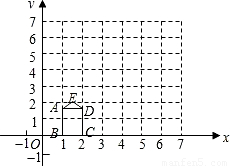 (2008•陕西)如图,矩形ABCD的长,宽分别为
(2008•陕西)如图,矩形ABCD的长,宽分别为 和1,且OB=1,点E(
和1,且OB=1,点E( ,2),连接AE,ED.
,2),连接AE,ED.