题目内容
如图,小李投掷铅球,如果铅球运行时离地面的高度y(米)关于水平距离x(米)的函数解析式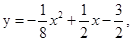 为什那么铅球运动过程中最高点离地面的距离____米。
为什那么铅球运动过程中最高点离地面的距离____米。
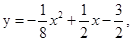 为什那么铅球运动过程中最高点离地面的距离____米。
为什那么铅球运动过程中最高点离地面的距离____米。
2.
试题分析:直接利用公式法求出函数的最值即可得出最高点离地面的距离.
∵函数解析式为:y=?
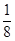 x2+
x2+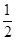 x+
x+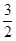 ,
,∴y最值=
 =
=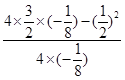 =2.
=2.故答案为:2.

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
题目内容
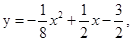 为什那么铅球运动过程中最高点离地面的距离____米。
为什那么铅球运动过程中最高点离地面的距离____米。
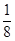 x2+
x2+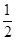 x+
x+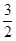 ,
, =
=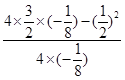 =2.
=2.
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案