题目内容
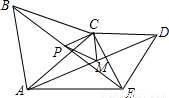
 如图,在线段AE同侧作两个等边三角形△ABC和△CDE(∠ACE<120°),点P与点M分别是线段BE和AD的中点,则△CPM是
如图,在线段AE同侧作两个等边三角形△ABC和△CDE(∠ACE<120°),点P与点M分别是线段BE和AD的中点,则△CPM是
- A.钝角三角形
- B.直角三角形
- C.等边三角形
- D.非等腰三角形
C
分析:首先根据等边三角形的性质,得出AC=BC,CD=CE,∠ACB=∠ECD=60°,则∠BCE=∠ACD,从而根据SAS证明△BCE≌△ACD,得∠CBE=∠CAD,BE=AD;再由点P与点M分别是线段BE和AD的中点,得BP=AM,根据SAS证明△BCP≌△ACM,得PC=MC,∠BCP=∠ACM,则∠PCM=∠ACB=60°,从而证明该三角形是等边三角形.
解答:∵△ABC和△CDE都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠ECD=60°.
∴∠BCE=∠ACD.
∴△BCE≌△ACD.
∴∠CBE=∠CAD,BE=AD.
又点P与点M分别是线段BE和AD的中点,
∴BP=AM.
∴△BCP≌△ACM.
∴PC=MC,∠BCP=∠ACM.
∴∠PCM=∠ACB=60°.
∴△CPM是等边三角形.
故选C.
点评:三角形中位线性质应用比较广泛,尤其是在三角形、四边形方面起着非常重要作用,本题结合三角形全等的知识,考查了中位线定理的应用.
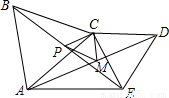
分析:首先根据等边三角形的性质,得出AC=BC,CD=CE,∠ACB=∠ECD=60°,则∠BCE=∠ACD,从而根据SAS证明△BCE≌△ACD,得∠CBE=∠CAD,BE=AD;再由点P与点M分别是线段BE和AD的中点,得BP=AM,根据SAS证明△BCP≌△ACM,得PC=MC,∠BCP=∠ACM,则∠PCM=∠ACB=60°,从而证明该三角形是等边三角形.
解答:∵△ABC和△CDE都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠ECD=60°.
∴∠BCE=∠ACD.
∴△BCE≌△ACD.
∴∠CBE=∠CAD,BE=AD.
又点P与点M分别是线段BE和AD的中点,
∴BP=AM.
∴△BCP≌△ACM.
∴PC=MC,∠BCP=∠ACM.
∴∠PCM=∠ACB=60°.
∴△CPM是等边三角形.
故选C.
点评:三角形中位线性质应用比较广泛,尤其是在三角形、四边形方面起着非常重要作用,本题结合三角形全等的知识,考查了中位线定理的应用.

练习册系列答案
相关题目
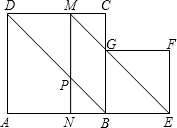 M,作MN⊥AB,垂足为N,MN交BD于点P.设正方形ABCD的边长为1.
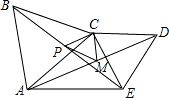
M,作MN⊥AB,垂足为N,MN交BD于点P.设正方形ABCD的边长为1.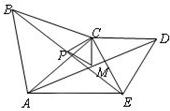 7、如图,在线段AE同侧作两个等边三角形△ABC和△CDE(∠ACE<120°),点P与点M分别是线段BE和AD的中点,则△CPM是( )
7、如图,在线段AE同侧作两个等边三角形△ABC和△CDE(∠ACE<120°),点P与点M分别是线段BE和AD的中点,则△CPM是( )