题目内容
小明在平面上标出了2007个点并画了一条直线L,他发现:这2007个点中的每一点关于直线L的对称点,仍在这2007个点中,请你说明:这2007个点中至少有1个点在直线L上.
分析:首先假设这2007个点都不在直线L上,得出每个点Ai(i=1,2,…,2007)关于直线L的对称点A′1仍在这2007个点中,
不在直线L上点Ai(i=1,2,,2007)与Ai关于直线L对称的点A′i成对出现,即平面上标出的点的总数应是偶数个,与点的总数2007相矛盾.
不在直线L上点Ai(i=1,2,,2007)与Ai关于直线L对称的点A′i成对出现,即平面上标出的点的总数应是偶数个,与点的总数2007相矛盾.
解答:证明:假设这2007个点都不在直线L上,
由于其中每个点Ai(i=1,2,…,2007)关于直线L的对称点A′1仍在这2007个点中,
所以A′i不在直线L上.
也就是说,不在直线L上点Ai(i=1,2,,2007)与Ai关于直线L对称的点A′i成对出现,
即平面上标出的点的总数应是偶数个,与点的总数2007相矛盾,
因此,“这2007个点都不在直线L上”的假设不能成立,即这2007个点中至少有1个点在直线L上.
由于其中每个点Ai(i=1,2,…,2007)关于直线L的对称点A′1仍在这2007个点中,
所以A′i不在直线L上.
也就是说,不在直线L上点Ai(i=1,2,,2007)与Ai关于直线L对称的点A′i成对出现,
即平面上标出的点的总数应是偶数个,与点的总数2007相矛盾,
因此,“这2007个点都不在直线L上”的假设不能成立,即这2007个点中至少有1个点在直线L上.
点评:此题主要考查了反证法的应用,从命题的反面出发,假设出2007个点都不在直线L上,根据平面上点的坐标性质得出矛盾,进而肯定命题正确是解决问题的关键.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
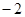 ;B袋中有三个完全相同的小球,分别标有数字
;B袋中有三个完全相同的小球,分别标有数字 ;B袋中有三个完全相同的小球,分别标有数字
;B袋中有三个完全相同的小球,分别标有数字