题目内容
【题目】已知:在平面直角坐标系中,抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,顶点为A.
,顶点为A.
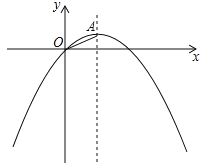
(1)求抛物线的表达式及顶点A的坐标;
(2)点P为抛物线对称轴上一点,联结OA、OP.
①当OA⊥OP时,求OP的长;
②过点P作OP的垂线交对称轴右侧的抛物线于点B,联结OB,当∠OAP=∠OBP时,求点B的坐标.
【答案】(1)顶点A的坐标为(2,1);(2)![]()
【解析】
试题分析:(1)根据抛物线对称轴列方程求出![]() ,即可得到抛物线解析式,再根据解析式写出顶点坐标;
,即可得到抛物线解析式,再根据解析式写出顶点坐标;
(2)设对称轴与![]() 轴的交点为E.①求出
轴的交点为E.①求出![]() ,然后根据锐角的正切值相等列出等式,再求解得到
,然后根据锐角的正切值相等列出等式,再求解得到![]() ,然后利用勾股定理列式计算即可;②过点B作AP的垂线,垂足为F,根据抛物线解析式设出点B的坐标,然后表示出
,然后利用勾股定理列式计算即可;②过点B作AP的垂线,垂足为F,根据抛物线解析式设出点B的坐标,然后表示出![]() ,在
,在![]() 和
和![]() 中,利用相等的锐角的正切值相等列式求出
中,利用相等的锐角的正切值相等列式求出![]() 再求出
再求出![]() 然后根据相似三角形对应边成比例列出比例式求解得到
然后根据相似三角形对应边成比例列出比例式求解得到![]() 的值,从而得解.
的值,从而得解.
试题解析:(1)![]() 抛物线
抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,
,![]()
![]() .
.
![]() 顶点A的坐标为(2,1);
顶点A的坐标为(2,1);
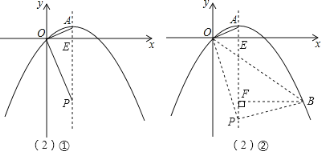
设对称轴与![]() 轴的交点为E.①如图,在直角三角形AOE和直角三角形POE中,
轴的交点为E.①如图,在直角三角形AOE和直角三角形POE中,![]()
![]()
![]()
![]()
![]()
![]()
![]() ;
;
②如图,过点B作AP的垂线,垂足为F,设点![]() ,
,![]()
![]()
![]() 在
在![]() 和
和![]() 中,
中,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
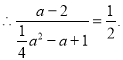 整理得:
整理得:![]() 解得
解得![]() (舍).
(舍).![]()

练习册系列答案
相关题目