题目内容
若分式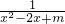 不论x取何值总有意义,则m的取值范围是
不论x取何值总有意义,则m的取值范围是
- A.m≥1
- B.m>1
- C.m≤1
- D.m<1
B
分析:主要求出当x为什么值时,分母不等于0.可以采用配方法整理成(a+b)2+k(k>0)的形式即可解决.
解答:分式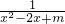 不论x取何值总有意义,则其分母必不等于0,
不论x取何值总有意义,则其分母必不等于0,
即把分母整理成(a+b)2+k(k>0)的形式为
(x2-2x+1)+m-1=(x-1)2+(m-1),
因为论x取何值(x2-2x+1)+m-1=(x-1)2+(m-1)都不等于0,
所以m-1>0,即m>1,
故选B.
点评:此题主要考查了分式的意义,要求掌握.意义:对于任意一个分式,分母都不能为0,否则分式无意义.当分母是个二项式时,分式有意义的条件时分母能整理成(a+b)2+k(k>0)的形式,即一个完全平方式与一个正数的和的形式.只有这样不论未知数取何值,式子(a+b)2+k(k>0)都不可能等于0.
分析:主要求出当x为什么值时,分母不等于0.可以采用配方法整理成(a+b)2+k(k>0)的形式即可解决.
解答:分式
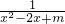 不论x取何值总有意义,则其分母必不等于0,
不论x取何值总有意义,则其分母必不等于0,即把分母整理成(a+b)2+k(k>0)的形式为
(x2-2x+1)+m-1=(x-1)2+(m-1),
因为论x取何值(x2-2x+1)+m-1=(x-1)2+(m-1)都不等于0,
所以m-1>0,即m>1,
故选B.
点评:此题主要考查了分式的意义,要求掌握.意义:对于任意一个分式,分母都不能为0,否则分式无意义.当分母是个二项式时,分式有意义的条件时分母能整理成(a+b)2+k(k>0)的形式,即一个完全平方式与一个正数的和的形式.只有这样不论未知数取何值,式子(a+b)2+k(k>0)都不可能等于0.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
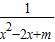 不论x取何值总有意义,则m的取值范围是( )
不论x取何值总有意义,则m的取值范围是( )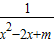 不论x取何值总有意义,则m的取值范围是( )
不论x取何值总有意义,则m的取值范围是( )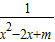 不论x取何值总有意义,则m的取值范围是( )
不论x取何值总有意义,则m的取值范围是( )