题目内容
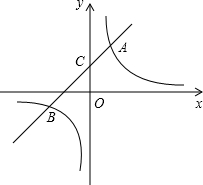 如图,反比例函数
如图,反比例函数 的图象与一次函数y=mx+b的图象交于两点A(1,3),B(n,-1).
的图象与一次函数y=mx+b的图象交于两点A(1,3),B(n,-1).
(1)求反比例函数与一次函数的函数关系式;
(2)求由A、B、O三点构成的三角形面积;
(3)在反比例函数的图象上另找点P,使得点A、O、P构成的三角形面积与A、B、O三点构成的三角形面积相等,这样的点还有几个?请直接写出个数.
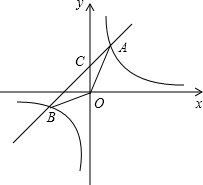 解:(1)∵点A(1,3)在反比例函数y=
解:(1)∵点A(1,3)在反比例函数y= 的图象上,
的图象上,∴k=1×3=3,
∴反比例函数的解析式为:y=
 ;
;把B(n,-1)代入y=
 得,n=
得,n=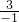 =-3,
=-3,∴点B的坐标为(-3,-1),
把A(1,3)、B(-3,-1)代入y=mx+b得
 ,
,解得
 ,
,故一次函数的函数关系式为:y=x+2;
(2)对于y=x+2,令x=0,则y=3,
则C点坐标为(0,2),
则S△AOB=S△OBC+S△AOC=
 ×2×3+
×2×3+ ×2×1=4;
×2×1=4;(3)设点P的坐标为:(a,
 ),
),当点P在第一象限,且在A点的右侧,即a>1,如图,
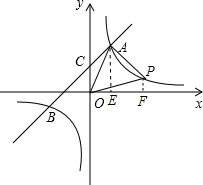 作AE⊥x轴于E,PF⊥x轴于F,
作AE⊥x轴于E,PF⊥x轴于F,∵S△AOP+S△OPF=S△AOE+S梯形AEFP,
而S△OPF=S△AOE,
∴S△AOP=S梯形AEFP=
 ×(
×( +3)×(a-1)=4,解得a1=3,a2=-
+3)×(a-1)=4,解得a1=3,a2=- ,
,∴a=3,此时P点坐标为(3,1);
当点P在第一象限,且在A点的右侧,即0<a<1,
S△AOP=S梯形AEFP=
 ×(
×( +3)×(1-a)=4,解得a1=-3,a2=
+3)×(1-a)=4,解得a1=-3,a2= ,
,则a=
 ,此时P点坐标为(
,此时P点坐标为( ,3);
,3);当点P在第三象限,即a<0,PA交y轴于H点,如图,
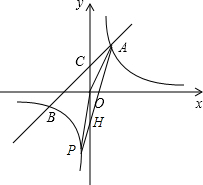
易求出直线PA的解析式为y=-
 x+
x+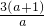 ,
,则H点坐标为(0,
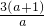 ),
),则S△AOP=S△OHP+S△OAH=
 (-a)•|
(-a)•|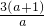 |+
|+ ×1×|
×1×|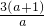 |=4,
|=4,当H点在x轴上方,
 (-a)•
(-a)•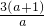 +
+ ×1×
×1×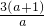 =4,解得a1=-3,a2=
=4,解得a1=-3,a2= ,
,故a=-3,此时P点与B点重合;
当H点在x轴下方,
 (-a)•[-
(-a)•[-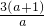 ]+
]+ ×1×[-
×1×[-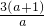 ]=4,解得a1=3,a2=-
]=4,解得a1=3,a2=- ,
,则a=-
 ,此时P点坐标为(-
,此时P点坐标为(- ,-3),
,-3),故满足条件的P点有三个:(3,1),(
 ,3),(-
,3),(- ,-3).
,-3).分析:(1)先把A(1,3)代入反比例函数解析式求出k,再把B(n,1)代入反比例函数解析式求出n,然后利用待定系数法确定一次函数y=mx+b的解析式;
(2)先确定C点坐标为(0,2),然后利用S△AOB=S△OBC+S△AOC进行计算;
(3)设点P的坐标为:(a,
 ),讨论:①当点P在第一象限,且在A点的右侧,即a>1,如图作AE⊥x轴于E,PF⊥x轴于F,易得S△AOP=S梯形AEFP=
),讨论:①当点P在第一象限,且在A点的右侧,即a>1,如图作AE⊥x轴于E,PF⊥x轴于F,易得S△AOP=S梯形AEFP= ×(
×( +3)×(a-1)=4,解得a1=3,a2=-
+3)×(a-1)=4,解得a1=3,a2=- ,满足条件P点坐标为(3,1);当点P在第一象限,且在A点的右侧,即0<a<1,S△AOP=S梯形AEFP=
,满足条件P点坐标为(3,1);当点P在第一象限,且在A点的右侧,即0<a<1,S△AOP=S梯形AEFP= ×(
×( +3)×(1-a)=4,解得a1=-3,a2=
+3)×(1-a)=4,解得a1=-3,a2= ,得到P点坐标为(
,得到P点坐标为( ,3);
,3);②当点P在第三象限,即a<0,PA交y轴于H点,利用待定系数法求出直线PA的解析式为y=-
 x+
x+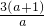 ,则H点坐标为(0,
,则H点坐标为(0,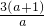 ),得到S△AOP=S△OHP+S△OAH=
),得到S△AOP=S△OHP+S△OAH= (-a)•|
(-a)•|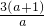 |+
|+ ×1×|
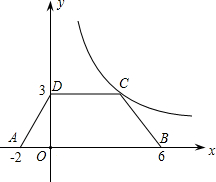
×1×|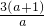 |=4,然后讨论H点在x轴上方或下方,去绝对值得到两个方程,解方程就可确定a的值,从而得到P点坐标.
|=4,然后讨论H点在x轴上方或下方,去绝对值得到两个方程,解方程就可确定a的值,从而得到P点坐标.点评:本题考查了反比例函数的综合题:点在反比例函数图象上,点的坐标满足其解析式;利用待定系数法求函数的解析式;运用分类讨论的方法去探究满足条件的点的个数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•南昌)如图,等腰梯形ABCD放置在平面坐标系中,已知A(-2,0)、B(6,0)、D(0,3),反比例函数的图象经过点C.
(2012•南昌)如图,等腰梯形ABCD放置在平面坐标系中,已知A(-2,0)、B(6,0)、D(0,3),反比例函数的图象经过点C. (2013•和平区一模)如图,反比例函数的图象经过点A、B,点A的坐标为(1,3),点B的纵坐标为1,点C的坐标为(2,0).
(2013•和平区一模)如图,反比例函数的图象经过点A、B,点A的坐标为(1,3),点B的纵坐标为1,点C的坐标为(2,0). (2012•湖里区一模)如图,反比例函数y=
(2012•湖里区一模)如图,反比例函数y=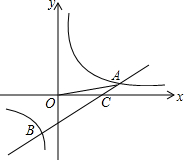 已知:如图,反比例函数的图象和一次函数的图象交于A和B两点,且点A的坐标为(3,1),点B的坐标为(-1,-3),一次函数图象与X轴交于点C.连接OA.
已知:如图,反比例函数的图象和一次函数的图象交于A和B两点,且点A的坐标为(3,1),点B的坐标为(-1,-3),一次函数图象与X轴交于点C.连接OA.