题目内容
观察：（x-1）（x+1）=x2-1；（x-1）（x2+x+1）=x3-1；（x-1）（x3+x2+x+1）=x4-1，则根据规律：（x-1）（x6+x5+x4+x3+x2+x+1）=________．
x7-1
分析：根据规律，最后结果是x的次数等于第二个括号x的最高指数加1次幂与1的差．
解答：∵（x-1）（x+1）=x2-1，
（x-1）（x2+x+1）=x3-1，
（x-1）（x3+x2+x+1）=x4-1，
以此类推，（x-1）（x6+x5+x4+x3+x2+x+1）=x7-1．
故答案为：x7-1．
点评：本题主要考查了平方差公式的推广运用，找出x指数的变化规律是解题的关键．
分析：根据规律，最后结果是x的次数等于第二个括号x的最高指数加1次幂与1的差．
解答：∵（x-1）（x+1）=x2-1，
（x-1）（x2+x+1）=x3-1，
（x-1）（x3+x2+x+1）=x4-1，
以此类推，（x-1）（x6+x5+x4+x3+x2+x+1）=x7-1．
故答案为：x7-1．
点评：本题主要考查了平方差公式的推广运用，找出x指数的变化规律是解题的关键．
练习册系列答案
第三学期赢在暑假系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
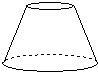15、请观察右图几何体，指出其主视图（从前面看）是（ ）
分析中，各年龄段发病的总人数如图所示（发病的病人年龄在0∽80岁之间），请你观察图形回答下面的问题．