题目内容
已知:矩形纸片ABCD中,AB=26厘米,BC=18.5厘米,点E在AD上,且AE=6厘米,点P是![]() 边上一动点.按如下操作:
边上一动点.按如下操作:
步骤一,折叠纸片,使点P与点![]() 重合,展开纸片得折痕MN(如图23(1)所示);
重合,展开纸片得折痕MN(如图23(1)所示);
步骤二,过点P作![]() ,交MN所在的直线于点Q,连接QE(如图23(2)所示)
,交MN所在的直线于点Q,连接QE(如图23(2)所示)
(1)无论点P在![]() 边上任何位置,都有PQ QE(填“
边上任何位置,都有PQ QE(填“![]() ”、“
”、“![]() ”、“
”、“![]() ”号);
”号);
(2)如图23(3)所示,将纸片ABCD放在直角坐标系中,按上述步骤一、二进行操作:
①当点![]() 在
在![]() 点时,PT与MN交于点Q1 ,Q1点的坐标是( , );
点时,PT与MN交于点Q1 ,Q1点的坐标是( , );
②当PA=6厘米时,PT与MN交于点Q2 ,Q2点的坐标是( , );
③当PA=12厘米时,在图22(3)中画出MN,PT(不要求写画法),并求出MN与PT的交点Q3的坐标;
(3)点![]() 在运动过程中,PT与MN形成一系列的交点Q1 ,Q2 ,Q3 ,…观察、猜想:众多的交点形成的图象是什么?并直接写出该图象的函数表达式.
在运动过程中,PT与MN形成一系列的交点Q1 ,Q2 ,Q3 ,…观察、猜想:众多的交点形成的图象是什么?并直接写出该图象的函数表达式.
 |

23(1) 23(2) 23(3)
(1)![]() =
= ![]()
①![]() 点的坐标是(0,3);
点的坐标是(0,3);
②![]() 点的坐标是(6,6);
点的坐标是(6,6);
 |
③依题意可知:![]()
![]()
![]()
![]()
![]() 与
与![]() 轴垂直,
轴垂直,
![]()
![]() 可证
可证![]() ,
,
![]()
![]() 是折痕
是折痕![]()
![]()
![]() ∽
∽![]()
![]()
![]()
![]()
![]()
![]()
![]()
(3)猜想:一系列的交点一系列的交点构成二次函数图象的一部分
![]() 解析式为:
解析式为:![]()

练习册系列答案
相关题目
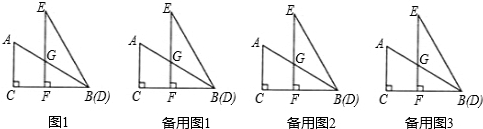


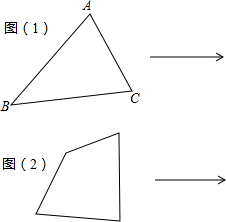
 (2012•路南区一模)已知:有一纸片如图,其中△ABC中,AD⊥BC,垂足为点D,BD=CD,点M在BA的延长线上.实施操作:将纸片沿一直线AN折叠,使AM和AC重合,并且过点C作CE⊥AN,垂足为点E.
(2012•路南区一模)已知:有一纸片如图,其中△ABC中,AD⊥BC,垂足为点D,BD=CD,点M在BA的延长线上.实施操作:将纸片沿一直线AN折叠,使AM和AC重合,并且过点C作CE⊥AN,垂足为点E.