题目内容
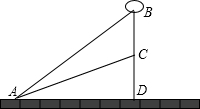
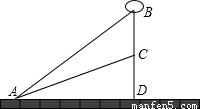
如图，在天桥广场上的A处放一气球，当气球上升了75m时，恰在旗杆CD的上空B处，在A点测得气球和C的仰角分别是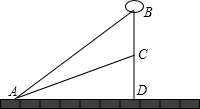
47°54′、25°17′，求旗杆CD的高（精确到0.01m）．
分析：设CD=x，根据BD和∠BAD即可求得AD的值，根据AD和∠CAD即可求得CD的值，即可解题．
解答：解：设CD=x，
∵BD=75，
∴AD=
=
≈67.768（m），
∴x=AD•tan∠CAD，
=67.768×tan25°17′≈32.01（m）．
答：旗杆CD的高约为32.01m．
∵BD=75，
∴AD=
| BD |
| tan∠BAD |
| 75 |
| tan47°54′ |
∴x=AD•tan∠CAD，
=67.768×tan25°17′≈32.01（m）．
答：旗杆CD的高约为32.01m．
点评：本题考查了三角函数值的计算，三角函数在直角三角形中的运用，本题中计算AD的值是解题的关键．
练习册系列答案
金博士一点全通系列答案
相关题目
47°54′、25°17′，求旗杆CD的高（精确到0.01m）．
