题目内容
【题目】如图直线AB、CD、EF相交于点O,是∠AOC的邻补角是 ,∠DOA的对顶角是 ,若∠AOC=50°,则∠BOD= 度,∠COB= 度.
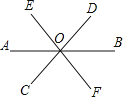
【答案】∠AOC的邻补角是∠BOC,∠AOD;∠DOA的对顶角是∠BOC;∠BOD=50°,∠COB=130°
【解析】
试题分析:邻补角必须是相邻的两个角,即有一条公共边和一个公共顶点的互补的两个角;对顶角拥有一个公共顶点,其中一个角的两条边是另一个角的两条边的反向延长线,对顶角的度数相等.
解:①∠AOC的邻补角是∠BOC,∠AOD;
②∠DOA的对顶角是∠BOC;
③若∠AOC=50°,而∠BOD是∠AOC的对顶角,
∠COB是∠AOC邻补角,根据性质可得:
∠BOD=50°,∠COB=130°.

练习册系列答案
相关题目