题目内容
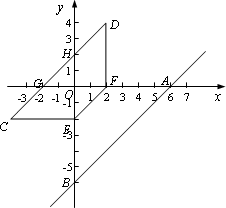
直线y=x-6与x轴、y轴分别交于点A、B,点E从B点,出发以每秒1个单位的速度沿线段BO向O点移动(与B、O点不重合),过E作EF∥AB,交x轴于F.将四边形ABEF沿EF折叠,得到四边形DCEF,设点E的运动时间为t秒.

(1)①直线y=x-6与坐标轴交点坐标是A(________,________),B(________,________);
②画出t=2时,四边形ABEF沿EF折叠后的图形(不写画法);
(2)若CD交y轴于H点,求证:四边形DHEF为平行四边形;并求t为何值时,四边形DHEF为菱形(计算结果不需化简);
(3)设四边形DCEF落在第一象限内的图形面积为S,求S关于t的函数表达式,并求出S的最大值.
解析:
|
解:(1)①直线 ②如图,四边形DCEF即为四边形ABEF沿EF折叠后的图形; 3分
(2)∵四边形DCEF与四边形ABEF关于直线EF对称, 又AB∥EF,∴CD∥EF. ∵OA=OB,∠AOB=90°,∴∠BAO=45°. ∵AB∥EF,∴∠AFE=135°. ∴∠DFE=∠AFE=135°. ∴∠AFD=360°-2×135°=90°,即DF⊥x轴. ∴DF∥EH,∴四边形DHEF为平行四边形. 5分 要使□DHEF为菱形,只需EF=DF,∵AB∥EF,∠FAB=∠EBA,∴FA=EB. ∴DF=FA=EB=t. 又∵OE=OF=6-t,∴EF= ∴ ∴ ∴当 (3)分两种情况讨论: ①当0<t≤3时, 8分 四边形DCEF落在第一象限内的图形是△DFG,∴S= ∵S= ②当3<t<6时, 10分 四边形DCEF落在第一象限内的图形是四边形DHOF, ∴S四边形DHOF=S△DGF-S△HGO. ∴S= = = ∵a= ∴S 有最大值.∴当 t=4时,S最大=6. 12分综上所述,当 S=4时,S最大值为6. 13分
|

 名校课堂系列答案
名校课堂系列答案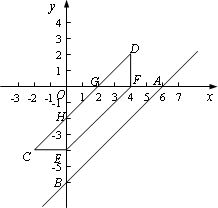
 ,AO⊥BO.D为线段MN的中点,OH为Rt△OPC斜边上的高.
,AO⊥BO.D为线段MN的中点,OH为Rt△OPC斜边上的高.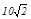 ,写出探索过程.
,写出探索过程.
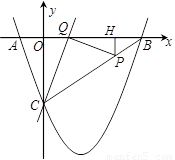
 x2+bx+c与坐标轴交于A、B、C三点, A点的坐标为(-1,0),过点C的直线y=
x2+bx+c与坐标轴交于A、B、C三点, A点的坐标为(-1,0),过点C的直线y= x-3与x轴交于点Q,点P是线段BC上的一个动点,过P作PH⊥OB于点H.若PB=5t,且0<t<1.
x-3与x轴交于点Q,点P是线段BC上的一个动点,过P作PH⊥OB于点H.若PB=5t,且0<t<1.
 x2+bx+c与坐标轴交于A、B、C三点, A点的坐标为
x2+bx+c与坐标轴交于A、B、C三点, A点的坐标为 x-3与x轴交于点Q,点P是线段BC上的一个动点,过P作PH⊥OB于点H.若PB=5t,且0<t<1.
x-3与x轴交于点Q,点P是线段BC上的一个动点,过P作PH⊥OB于点H.若PB=5t,且0<t<1.