题目内容
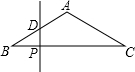 (2011•通州区二模)如图,已知△ABC中,AB=AC=2,∠B=30°,P是BC边上一个动点,过点P作PD⊥BC,交△ABC其他边于点D.若设PB为x,△BPD的面积为y,则y与x之间的函数关系的图象大致是( )
(2011•通州区二模)如图,已知△ABC中,AB=AC=2,∠B=30°,P是BC边上一个动点,过点P作PD⊥BC,交△ABC其他边于点D.若设PB为x,△BPD的面积为y,则y与x之间的函数关系的图象大致是( )分析:△BDP的面积=
BP×DP,通过题干已知条件,用x分别表示出BP、DP,根据所得的函数,利用其图象,可分两种情况解答:(1)0<x≤1;(2)1<x<2.
| 1 |
| 2 |
解答:解:(1)当0<x≤1时,在△ABC中,AB=AC=2,∠B=30°,PD⊥BC,
∴PD=
x;
∴y=
BP×DP=
x2(0<x≤1),
∵
>0,∴函数图象开口向上;
(2)当1<x<2,同理证得PD=
(2
-x)=2-
x;
∴y=
BP×DP=
x×(2-
x),
y=-
x2+x;
∵-
<0,
∴函数图象开口向下;
综上,答案C的图象大致符合.
故选C.
∴PD=
| ||
| 3 |
∴y=
| 1 |
| 2 |
| ||
| 6 |
∵
| ||
| 6 |
(2)当1<x<2,同理证得PD=
| ||
| 3 |
| 3 |
| ||
| 3 |
∴y=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 3 |
y=-
| ||
| 6 |
∵-
| ||
| 6 |
∴函数图象开口向下;
综上,答案C的图象大致符合.
故选C.
点评:本题考查了二次函数的图象,考查了学生从图象中读取信息的数形结合能力,体现了分类讨论的思想.

练习册系列答案
相关题目
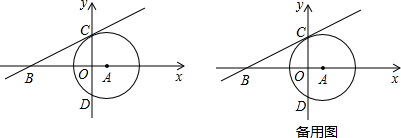 (2011•通州区二模)已知:如图,⊙A与y轴交于C、D两点,圆心A的坐标为(1,0),⊙A的半径为
(2011•通州区二模)已知:如图,⊙A与y轴交于C、D两点,圆心A的坐标为(1,0),⊙A的半径为