题目内容
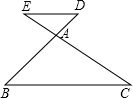已知：如图，ED∥BC，则AE：AD等于（ ）| A、AC：AB | B、AB：AC | C、DE：BC | D、BA：BD |
分析：由ED与BC平行，得到两对内错角相等，再利用两对对应角相等的两三角形相似，可得三角形AED与三角形ACB相似，根据相似得比例，变形后可得所求．
解答：解：∵ED∥BC，
∴∠E=∠C，∠D=∠B，
∴△AED∽△ACB，
∴
=
，
即AE：AD=AC：AB．
故选A
∴∠E=∠C，∠D=∠B，
∴△AED∽△ACB，
∴
| AE |
| AC |
| AD |
| AB |
即AE：AD=AC：AB．
故选A
点评：此题考查了相似三角形的判定与性质，比较简单．解答时注意对应点与对应边要对应写准．
练习册系列答案
相关题目
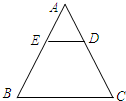已知，如图，ED∥BC，且
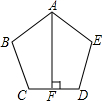已知，如图，AB=AE，BC=ED，∠B=∠E，AF⊥CD，F为垂足，求证：FC=FD．
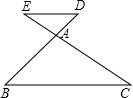已知：如图，ED∥BC，则AE：AD等于
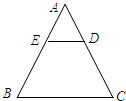已知，如图，ED∥BC，且
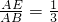，则
=________．