题目内容
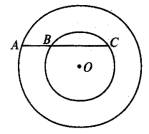
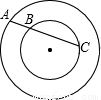
如图，两个同心圆，过大圆上一点A作小圆的割线，交小圆于B、C两点，且图中圆环的面积为4π，则AB•AC= ．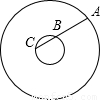
【答案】分析：首先，设圆心为O点，做AD与小圆相切，切点为点M，与大圆交于点D，连接OM，然后根据垂径定理和勾股定理推出AM2=OA2-OM2，既而推出AM2的值，结合割线和切线的性质即可得出结论．
解答：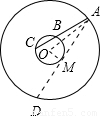
解：设圆心为O点，做AD与小圆相切，切点为点M，与大圆交于点D，连接OM，
∴OM⊥AD，
∴AM2=OA2-OM2，
∵πOA2-πOM2=4π，
∴AM2=4，
∵AM2=AB•AC，
∴AB•AC=4．
故答案为4．
点评：本题主要考查切线的性质、勾股定理、割线的性质、垂径定理，关键在于作辅助线AD、OM．
解答：
解：设圆心为O点，做AD与小圆相切，切点为点M，与大圆交于点D，连接OM，∴OM⊥AD，
∴AM2=OA2-OM2，
∵πOA2-πOM2=4π，
∴AM2=4，
∵AM2=AB•AC，
∴AB•AC=4．
故答案为4．
点评：本题主要考查切线的性质、勾股定理、割线的性质、垂径定理，关键在于作辅助线AD、OM．
练习册系列答案
相关题目
10、如图，两个同心圆，过大圆上一点A作小圆的割线，交小圆于B、C两点，且图中圆环的面积为4π，则AB•AC=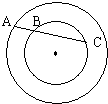
12、如图，两个同心圆，过大圆上一点A作小圆的割线交小圆于B、C两点，且AB•AC=4，则图中圆环的面积为
