题目内容
⊙O中，OD⊥AB，∠AOD=50°，C是圆周上一点，则∠BCD=
- A.50°
- B.25°
- C.30°
- D.40°
B
分析：由⊙O中，OD⊥AB，根据垂径定理，即可得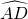
=
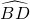，又由圆周角定理，可得∠BCD=
∠AOD，则可求得答案．
解答：∵⊙O中，OD⊥AB，
∴=，
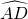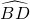∴∠BCD=∠AOD=×50°=25°．
故选B．
点评：此题考查了垂径定理与圆周角定理．此题难度不大，解题的关键是注意数形结合思想的应用．
分析：由⊙O中，OD⊥AB，根据垂径定理，即可得
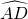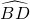=，又由圆周角定理，可得∠BCD=∠AOD，则可求得答案．解答：∵⊙O中，OD⊥AB，
∴
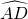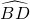=，∴∠BCD=
∠AOD=×50°=25°．故选B．
点评：此题考查了垂径定理与圆周角定理．此题难度不大，解题的关键是注意数形结合思想的应用．
练习册系列答案
相关题目
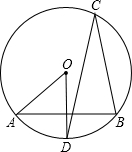⊙O中，OD⊥AB，∠AOD=50°，C是圆周上一点，则∠BCD=（ ）| A、50° | B、25° | C、30° | D、40° |
31、如图所示，在⊙O中，OD⊥AB于P，AP=4cm，PD=2cm，则OP的长等于（ ）
