题目内容
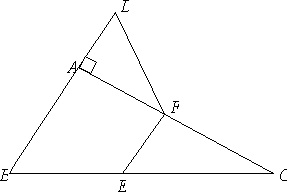
如图,已知:在△ABC中,∠BAC=90°,延长BA到点D,使AD=![]() AB,点G、E、F分别为边AB、BC、AC的中点.求证:DF=BE.
AB,点G、E、F分别为边AB、BC、AC的中点.求证:DF=BE.
答案:
解析:
解析:
|
解:因为AD= |

练习册系列答案
相关题目
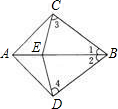
 如图,已知:在Rt△ABC中,∠C=90°,E为AB的中点,且DE⊥AB于E,若∠CAD:∠DAB=1﹕2,求∠B的度数.
如图,已知:在Rt△ABC中,∠C=90°,E为AB的中点,且DE⊥AB于E,若∠CAD:∠DAB=1﹕2,求∠B的度数.

