题目内容
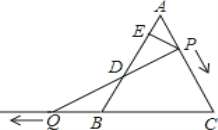
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=50°时,求∠DEF的度数.

【答案】(1)证明见解析;(2)65°
【解析】试题分析:⑴由AB=AC,可知∠B=∠ C,根据题意易得△ BDE ≌ △ CEF(SAS),从而得到DE=EF,命题得证.
⑵因为∠ A=50°,所以∠ B=∠ C=65°,由⑴可知,∠BDE=∠CEF,所以∠DEB+∠CEF=
∠DEB+∠ BDE=115°,从而∠ DEF=180°-115°=65°.
试题解析:⑴∵ AB=AC,∴ ∠B=∠ C.
在△ BDE和△ CEF中,
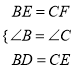 ,
,
∴ △ BDE ≌ △ CEF(SAS),则DE=EF,故△ DEF是等腰三角形.
⑵在△ABC中,∵∠A=50°,∴∠B=∠C=65°.
∵ △ BDE ≌ △ CEF,∴ ∠BDE=∠CEF,
∴ ∠DEB+∠CEF=∠DEB+∠ BDE=180°-65°=115°,
则 ∠ DEF=180°-(∠DEB+∠CEF)=180°-115°=65°.

练习册系列答案
相关题目
【题目】在检测一批刚出厂的足球的质量时,随机抽取了4个足球来测量其质量,把超过标准质量的克数记为正数,不足标准质量的克数记为负数,检测结果如下表:
足球的编号 | 1 | 2 | 3 | 4 |
与标准质量的差(克) | +3 | +2 | ﹣1 | ﹣2 |
则生产较合格的足球的编号是( )
A.1号B.2号C.3号D.4号