题目内容
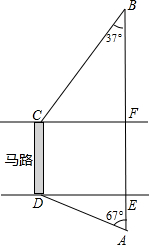 (2013•青岛)如图,马路的两边CF,DE互相平行,线段CD为人行横道,马路两侧的A,B两点分别表示车站和超市.CD与AB所在直线互相平行,且都与马路的两边垂直,马路宽20米,A,B相距62米,∠A=67°,∠B=37°.
(2013•青岛)如图,马路的两边CF,DE互相平行,线段CD为人行横道,马路两侧的A,B两点分别表示车站和超市.CD与AB所在直线互相平行,且都与马路的两边垂直,马路宽20米,A,B相距62米,∠A=67°,∠B=37°.(1)求CD与AB之间的距离;
(2)某人从车站A出发,沿折线A→D→C→B去超市B.求他沿折线A→D→C→B到达超市比直接横穿马路多走多少米.
(参考数据:sin67°≈
| 12 |
| 13 |
| 5 |
| 13 |
| 12 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
| 3 |
| 4 |
分析:(1)设CD与AB之间的距离为x,则在Rt△BCF和Rt△ADE中分别用x表示BF,AE,又AB=AE+EF+FB,代入即可求得x的值;
(2)在Rt△BCF和Rt△ADE中,分别求出BC、AD的长度,求出AD+DC+CB-AB的值即可求解.
(2)在Rt△BCF和Rt△ADE中,分别求出BC、AD的长度,求出AD+DC+CB-AB的值即可求解.
解答:解:(1)CD与AB之间的距离为x,
则在Rt△BCF和Rt△ADE中,
∵
=tan37°,
=tan67°,
∴BF=
≈
x,AE=
≈
x,
又∵AB=62,CD=20,
∴
x+
x+20=62,
解得:x=24,
答:CD与AB之间的距离约为24米;
(2)在Rt△BCF和Rt△ADE中,
∵BC=
≈
=40,
AD=
≈
=26,
∴AD+DC+CB-AB=40+20+26-62=24(米),
答:他沿折线A→D→C→B到达超市比直接横穿马路多走约24米.
则在Rt△BCF和Rt△ADE中,
∵
| CF |
| BF |
| DE |
| EA |
∴BF=
| CF |
| tan37° |
| 4 |
| 3 |
| DE |
| tan67° |
| 5 |
| 12 |
又∵AB=62,CD=20,
∴
| 4 |
| 3 |
| 5 |
| 12 |
解得:x=24,
答:CD与AB之间的距离约为24米;
(2)在Rt△BCF和Rt△ADE中,
∵BC=
| CF |
| sin37° |
| 24 | ||
|
AD=
| DE |
| sin67° |
| 24 | ||
|
∴AD+DC+CB-AB=40+20+26-62=24(米),
答:他沿折线A→D→C→B到达超市比直接横穿马路多走约24米.
点评:本题考查了解直角三角形,难度适中,解答本题的关键是在直角三角形中运用解直角三角形的知识求出各边的长度.

练习册系列答案
相关题目
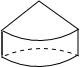 (2013•青岛)如图所示的几何体的俯视图是( )
(2013•青岛)如图所示的几何体的俯视图是( )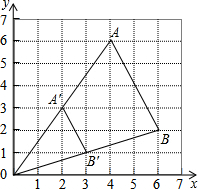 (2013•青岛)如图,△ABO缩小后变为△A′B′O,其中A、B的对应点分别为A′、B′点A、B、A′、B′均在图中在格点上.若线段AB上有一点P(m,n),则点P在A′B′上的对应点P′的坐标为( )
(2013•青岛)如图,△ABO缩小后变为△A′B′O,其中A、B的对应点分别为A′、B′点A、B、A′、B′均在图中在格点上.若线段AB上有一点P(m,n),则点P在A′B′上的对应点P′的坐标为( )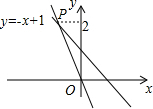 (2013•青岛)如图,一个正比例函数图象与一次函数y=-x+1的图象相交于点P,则这个正比例函数的表达式是
(2013•青岛)如图,一个正比例函数图象与一次函数y=-x+1的图象相交于点P,则这个正比例函数的表达式是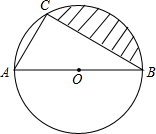 (2013•青岛)如图,AB是⊙O的直径,弦AC=2,∠ABC=30°,则图中阴影部分的面积是
(2013•青岛)如图,AB是⊙O的直径,弦AC=2,∠ABC=30°,则图中阴影部分的面积是