题目内容
 如图,已知第一象限的双曲线与正方形ACOE的两边相交于D,B两点,直线
如图,已知第一象限的双曲线与正方形ACOE的两边相交于D,B两点,直线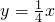 经过B点.则AD:DE的值是
经过B点.则AD:DE的值是
- A.3
- B.4
- C.2.5
- D.3.5
A
分析:设B(a, a),则OC=AC=AE=OE=a,设双曲线的解析式是y=
a),则OC=AC=AE=OE=a,设双曲线的解析式是y= ,把B的坐标代入求出k,得出y=
,把B的坐标代入求出k,得出y= ,把D的纵坐标a代入双曲线的解析式求出D的横坐标,求出DE、AD的值,代入AD:DE即可求出答案.
,把D的纵坐标a代入双曲线的解析式求出D的横坐标,求出DE、AD的值,代入AD:DE即可求出答案.
解答:∵直线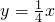 经过B点,
经过B点,
∴设B(a, a),则OC=AC=AE=OE=a,
a),则OC=AC=AE=OE=a,
设双曲线的解析式是y= ,
,
把B的坐标代入得:k= a2,
a2,
即y= ,
,
∵正方形OCAE,D在AE上,
∴D的纵坐标是a,
∵把y=a代入双曲线的解析式得:a= ,
,
解得:x= a,
a,
即DE= a,AD=a-
a,AD=a- a=
a= a,
a,
∴AD:DE=( a):(
a):( a)=3:1=3,
a)=3:1=3,
故选A.
点评:本题考查了用待定系数法求反比例函数的解析式和正方形性质的应用,关键是根据B的坐标求出AD、DE的值,题目比较典型,是一道比较好的题目.
分析:设B(a,
 a),则OC=AC=AE=OE=a,设双曲线的解析式是y=
a),则OC=AC=AE=OE=a,设双曲线的解析式是y= ,把B的坐标代入求出k,得出y=
,把B的坐标代入求出k,得出y= ,把D的纵坐标a代入双曲线的解析式求出D的横坐标,求出DE、AD的值,代入AD:DE即可求出答案.
,把D的纵坐标a代入双曲线的解析式求出D的横坐标,求出DE、AD的值,代入AD:DE即可求出答案.解答:∵直线
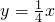 经过B点,
经过B点,∴设B(a,
 a),则OC=AC=AE=OE=a,
a),则OC=AC=AE=OE=a,设双曲线的解析式是y=
 ,
,把B的坐标代入得:k=
 a2,
a2,即y=
 ,
,∵正方形OCAE,D在AE上,
∴D的纵坐标是a,
∵把y=a代入双曲线的解析式得:a=
 ,
,解得:x=
 a,
a,即DE=
 a,AD=a-
a,AD=a- a=
a= a,
a,∴AD:DE=(
 a):(
a):( a)=3:1=3,
a)=3:1=3,故选A.
点评:本题考查了用待定系数法求反比例函数的解析式和正方形性质的应用,关键是根据B的坐标求出AD、DE的值,题目比较典型,是一道比较好的题目.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
 (2013•乐山)如图,已知第一象限内的点A在反比例函数y=
(2013•乐山)如图,已知第一象限内的点A在反比例函数y= 如图,已知第一象限的双曲线与正方形ACOE的两边相交于D,B两点,直线
如图,已知第一象限的双曲线与正方形ACOE的两边相交于D,B两点,直线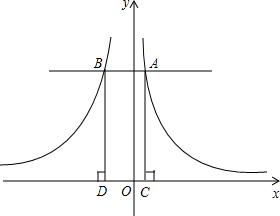 (2012•苏州)如图,已知第一象限内的图象是反比例函数y=
(2012•苏州)如图,已知第一象限内的图象是反比例函数y= 经过B点.则AD:DE的值是( )
经过B点.则AD:DE的值是( )