题目内容
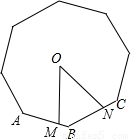
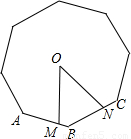
点M、N分别是正八边形相邻的边AB、BC上的点，且AM=BN，点O是正八边形的中心，则∠MON= 度．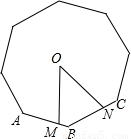
【答案】分析：由于正八边形是中心对称图形，中心角为360°÷8=45°，由题意知∠MON等于中心角的度数．
解答：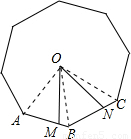
解：连接OA、OB、OC；
∵正八边形是中心对称图形，
∴中心角为360°÷8=45°；
∴∠OAM=∠OBN=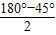
67.5°，
∵OA=OB，∠OAM=∠OBN，AM=BN，
∴△OAM≌△OBN，
∴∠AOM=∠BON，
∴∠MOB=∠NOC；
∵∠AOC=∠AOM+∠MOB+∠BON+∠NOC=90°，
∴∠MON=∠MOB+∠NOB=
（∠AOM+∠MOB+∠NOB+∠NOC）=
∠AOC=45°．
点评：本题利用了正八边形是中心对称图形求解．
解答：
解：连接OA、OB、OC；∵正八边形是中心对称图形，
∴中心角为360°÷8=45°；
∴∠OAM=∠OBN=
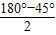67.5°，∵OA=OB，∠OAM=∠OBN，AM=BN，
∴△OAM≌△OBN，
∴∠AOM=∠BON，
∴∠MOB=∠NOC；
∵∠AOC=∠AOM+∠MOB+∠BON+∠NOC=90°，
∴∠MON=∠MOB+∠NOB=
（∠AOM+∠MOB+∠NOB+∠NOC）=∠AOC=45°．点评：本题利用了正八边形是中心对称图形求解．
练习册系列答案
相关题目
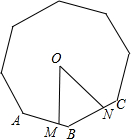点M、N分别是正八边形相邻的边AB、BC上的点，且AM=BN，点O是正八边形的中心，则∠MON=
3、如图所示，点M，N分别是正八边形相邻两边AB，BC上的点，且AM=BN，则∠MON=
