题目内容
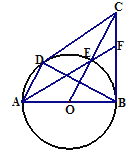
【题目】如图，已知AB为⊙O的直径，CD、CB为⊙O的切线，D、B为切点，OC交⊙O于点E，AE的延长线交BC于点F，连接AD、BD.给出以下结论：①AD∥OC；②FC=FE；③点E为△CDB的内心.其中正确的是________________（填序号）
【答案】①、③.
【解析】
试题分析：①连接OD，DE，EB．CD与BC是⊙O的切线，易证△CDO≌△CBO，则∠DCO=∠BCO．故OC⊥BD．
∵AB是直径， ∴AD⊥BD， ∴AD∥OC，故①正确；
③∵CD是⊙O的切线， ∴∠CDE=
∠DOE，而∠BDE=∠BOE，∴∠CDE=∠BDE，
即DE是∠CDB的角平分线，同理可证得BE是∠CBD的平分线，因此E为△CBD的内心，故③正确；
②若FC=FE，则应有∠OCB=∠CEF，应有∠CEF=∠AEO=∠EAB=∠DBA=∠DEA，
∴弧AD=弧BE，而弧AD与弧BE不一定相等，故②不正确；
练习册系列答案
相关题目
