题目内容
(本题8分) 已知一元二次方程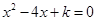 有两个不相等的实数根.
有两个不相等的实数根.
[小题1:(1)求 的取值范围;
的取值范围;
小题2:(2)如果 是符合条件的最大整数,且一元二次方程
是符合条件的最大整数,且一元二次方程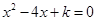 与
与 有一个相同的根,求此时
有一个相同的根,求此时 的值.
的值.
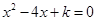 有两个不相等的实数根.
有两个不相等的实数根.[小题1:(1)求
 的取值范围;
的取值范围;小题2:(2)如果
 是符合条件的最大整数,且一元二次方程
是符合条件的最大整数,且一元二次方程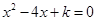 与
与 有一个相同的根,求此时
有一个相同的根,求此时 的值.
的值.小题1:[(1)

小题2:(2)
 或
或
考点:
解:(1)因为:一元二次方程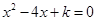 有两个不相等的实数根
有两个不相等的实数根
所以: ,
,
解得:
(2)因为:如果 是符合条件的最大整数
是符合条件的最大整数
所以 =3.
=3.
从而: ,故有:
,故有:
又因为:一元二次方程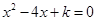 与
与 有一个相同的根
有一个相同的根
当根为 时,
时, ,解得:
,解得:
当根为 时,
时, ,解得:
,解得:
所以 或
或
点评:解决本题的关键根的判别式。
解:(1)因为:一元二次方程
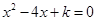 有两个不相等的实数根
有两个不相等的实数根所以:
 ,
,解得:

(2)因为:如果
 是符合条件的最大整数
是符合条件的最大整数所以
 =3.
=3.从而:
 ,故有:
,故有:
又因为:一元二次方程
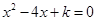 与
与 有一个相同的根
有一个相同的根当根为
 时,
时, ,解得:
,解得:
当根为
 时,
时, ,解得:
,解得:
所以
 或
或
点评:解决本题的关键根的判别式。

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 (2)解方程:
(2)解方程:
 时,出现滞销,便以定价的5折售完剩余的手链,试问该老板第二次售手链是赔钱了,还是赚钱了(不考虑其它因素)?若赔钱,赔多少?,若赚钱,赚多少?
时,出现滞销,便以定价的5折售完剩余的手链,试问该老板第二次售手链是赔钱了,还是赚钱了(不考虑其它因素)?若赔钱,赔多少?,若赚钱,赚多少?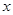 的一元二次方程
的一元二次方程 的一个根为0,则
的一个根为0,则 的值为( )
的值为( ) 



 的方程
的方程 .
.  的方程
的方程 的一个根为
的一个根为 ,则实数
,则实数 的值为( )
的值为( )

 花卉产
花卉产 业已成为我省许多地区经济发展的重要项目.近年来某乡的花卉产值不断增加,2003年花卉的产值是640万元,2005年产值达到l000万元.
业已成为我省许多地区经济发展的重要项目.近年来某乡的花卉产值不断增加,2003年花卉的产值是640万元,2005年产值达到l000万元.